e use the notation of the problem
(
Smooth optimization problem
).
Note that (1) implies that the proposition
(
Fritz John conditions
) cannot take
place with
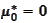 .
The conditions (2),(3) imply that the components of
.
The conditions (2),(3) imply that the components of
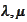 are "informative" in the sense that the set
are "informative" in the sense that the set
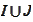 of the proposition (
Fritz John
conditions
) is nonempty and the non-zero components of
of the proposition (
Fritz John
conditions
) is nonempty and the non-zero components of
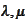 mark those conditions
mark those conditions
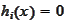 and
and
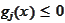 that are "active"
(
that are "active"
(
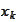 of the proposition (
Fritz John
conditions
)'s proof violates these conditions and the
of the proposition (
Fritz John
conditions
)'s proof violates these conditions and the
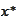 lies on the boundary set by such conditions).
lies on the boundary set by such conditions).
We introduce the
notation
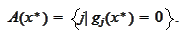 The condition 2 of the above definition may be equivalently written as
The condition 2 of the above definition may be equivalently written as
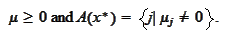
Here the
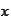 -sign
after the brackets
-sign
after the brackets
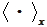 indicates that the summation of the scalar product is applied to the
components of the gradient
indicates that the summation of the scalar product is applied to the
components of the gradient
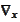 .
.
Proof
We assume that all the conditions of the definition
(
Pseudonormality
) hold and reach a
contradiction.
We introduce the
notation
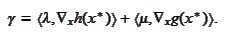 According to the condition 4 of this proposition and condition 2 of the
definition (
Pseudonormality
), there exists a
According to the condition 4 of this proposition and condition 2 of the
definition (
Pseudonormality
), there exists a
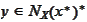 such
that
such
that
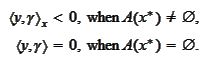 The condition 1 of the definition
(
Pseudonormality
) requires
that
The condition 1 of the definition
(
Pseudonormality
) requires
that
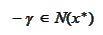 thus
thus
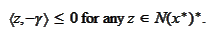 Hence, we already proven the statement for the case
Hence, we already proven the statement for the case
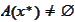 .
.
It remains to consider the case
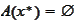 under the assumption that the conditions 1,2,3 of of the definition
(
Pseudonormality
) and the conditions 1,2,3,4
of this proposition are true and arrive to contradiction. By the assumption
under the assumption that the conditions 1,2,3 of of the definition
(
Pseudonormality
) and the conditions 1,2,3,4
of this proposition are true and arrive to contradiction. By the assumption
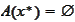 ,
we have
,
we have
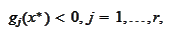 and by condition 2 of the definition
(
Pseudonormality
) we have
and by condition 2 of the definition
(
Pseudonormality
) we have
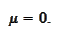 The condition 1 of the definition
(
Pseudonormality
) implies
The condition 1 of the definition
(
Pseudonormality
) implies
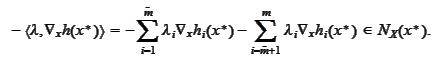 Hence, by the condition 2 of the proposition, all
Hence, by the condition 2 of the proposition, all
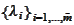 are
zero:
are
zero:
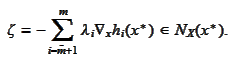 By the condition 3 there is a
By the condition 3 there is a
 from the interior of
from the interior of
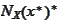 such that
such that
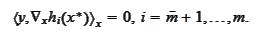 Hence,
Hence,
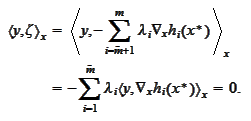 Hence, we have found a point
Hence, we have found a point
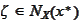 and an interior point
and an interior point
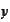 of
of
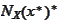 such
that
such
that
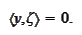 This is a contradiction. For an interior point of a cone
This is a contradiction. For an interior point of a cone
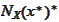 we must
have
we must
have
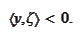
|