he following is an extremely efficient integration
formula:
|
|
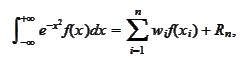
(Gauss-Hermite Intergration)
|
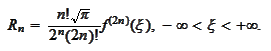Note that one can do the change of function
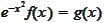to obtain more generic looking result.
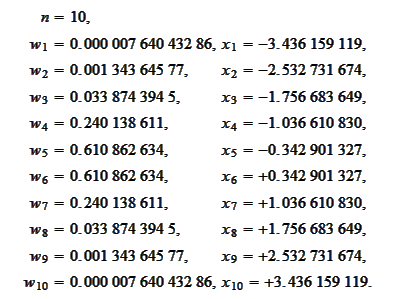
The below values of
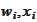are taken from
[Abramowitz]
, pages 890 and
924:
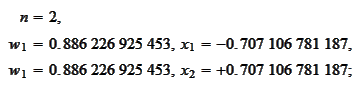
What follows next is a fragment of theory of orthogonal polynomials that leads
to the formula (
Gauss-Hermite
Integration
). The proposition
(
Gaussian quadrature rule
) provides
the justification. There are several sections after
(
Gaussian quadrature rule
) included
for their importance for other applications within these Notes. The reference
is
[Gautschi]
.
|
