Quantitative Analysis
Parallel Processing
Numerical Analysis
C++ Multithreading
Python for Excel
Python Utilities
Services
Author
Printable PDF file
I. Basic math.
II. Pricing and Hedging.
III. Explicit techniques.
IV. Data Analysis.
V. Implementation tools.
1. Finite differences.
2. Gauss-Hermite Integration.
A. Gram-Schmidt orthogonalization.
B. Definition and existence of orthogonal polynomials.
C. Three-term recurrence relation for orthogonal polynomials.
D. Orthogonal polynomials and quadrature rules.
E. Extremal properties of orthogonal polynomials.
F. Chebyshev polynomials.
3. Asymptotic expansions.
4. Monte-Carlo.
5. Convex Analysis.
VI. Basic Math II.
VII. Implementation tools II.
VIII. Bibliography
Notation. Index. Contents.

Orthogonal polynomials and quadrature rules.


efinition

(Quadrature rule) Let MATH and MATH are arbitrary numbers and $d\lambda$ is a measure on $\QTR{cal}{R}$ . We introduce the notations MATH The "quadrature rule"

MATH (Quadrature rule 1)
is said to have "degree of exactness" $d$ iff MATH The "precise degree of exactness" is the maximal degree of exactness.

The quadrature rule with degree of exactness $n-1$ is called "interpolatory".

Definition

(Lagrange interpolation formula) For a set MATH we define MATH according to the relationship

MATH (Lagrange interpolation formula 1)

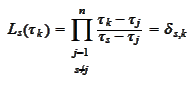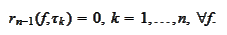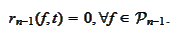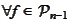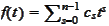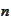Note that MATH hence MATH Therefore MATH Indeed, MATH has the form MATH . It is defined by values in $n$ distinct points.

Proposition

(Coefficients of quadrature rule) For a given set 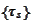MATH there exist 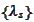MATH such that the quadrature rule ( Quadrature rule 1 ) is interpolatory.

Proof

Integrate the formula ( Lagrange interpolation formula 1 ).

Proposition

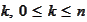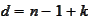(Higher degree of exactness) Given an integer $k,~0\leq k\leq n$ , the formula ( Quadrature rule 1 ) has degree of exactness $d=n-1+k$ iff both of the following conditions are satisfied:

1. The formula ( Quadrature rule 1 ) is interpolatory.

2. The polynomial 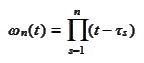MATH satisfies MATH

Proof

(Necessity) The claim (1) follows immediately by the definition ( Quadrature rule ).

The claim (2) follows by substitution $f=$ $\omega_{n}p$ into the formula ( Quadrature rule 1 ): MATH The term MATH is zero because MATH and term MATH is zero because MATH .

(Sufficiency) We assume (1),(2) and proceed to show that MATH We divide MATH by $\omega_{n}$ and represent the result as MATH where MATH and MATH . Then MATH The term MATH is zero by (2). Thus MATH and MATH because MATH and (1). We conclude MATH since MATH .

Proposition

(Gaussian quadrature rule) Let MATH be the polynomials related to measure $d\lambda$ as in the definition ( Orthogonal polynomials ) and the inner product MATH is positive definite. Then the formula ( Quadrature rule 1 ) has degree of exactness $2n-1$ iff $\omega_{n}=\pi_{n}$ and $\tau_{s}$ are zeros of $\pi_{n}$ .

Proof

We apply the proposition ( Higher degree of exactness ). The condition (2) requires that $\omega_{n}=\pi_{n}$ and $\tau_{s}$ are zeros of $\pi_{n}$ by definition of $\omega_{n}$ . The numbers MATH are all real by the proposition ( Zeros of orthogonal polynomials ).

The condition (1) becomes evident after noting similarity in structure of the polynomial $\omega_{n}$ and the polynomial $L_{\cdot}$ of the definition ( Lagrange interpolation formula ).

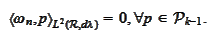
The coefficients 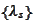MATH may be found from the proposition ( Coefficients of quadrature rule ).





Notation. Index. Contents.


















Copyright 2007