iven a set
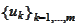(finite or infinite
)
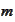of linearly independent elements of a linear space and a scalar product
,
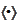the Gram-Schmidt orthogonalization procedure delivers a set
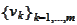of
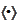-orthogonal
elements such
that
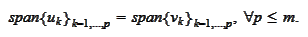
We start by
setting
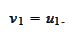For
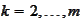we subtract from
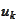the projection on
:
|
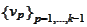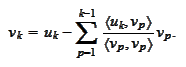
