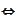 - if and only if.
- if and only if.
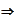 - hence.
- hence.
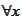 - for all
- for all
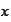 .
.
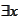 - there exists
- there exists
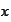 .
.
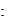 -
such that.
-
such that.
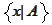 - set of
- set of
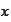 such that
such that
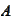 takes place.
takes place.
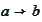 -
-
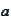 converges to
converges to
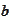 .
.
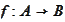 -
-
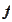 acts from
acts from
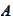 to
to
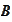 .
.
![$\left[ U\right] $](graphics/notesCF__0__18.gif) -
jump of
-
jump of
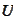 .
.
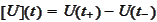 .
.
![$\left[ x\right] $](graphics/notesCF__0__21.gif) - integer part of real number
- integer part of real number
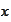 .
.
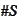 - the number of elements in the set
- the number of elements in the set
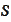 .
.
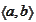 -scalar
product of
-scalar
product of
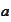 and
and
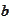 or
or
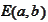 with
with
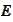 being mathematical expectation or duality action of
being mathematical expectation or duality action of
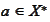 on
on
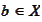 .
.
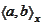 -scalar
product of
-scalar
product of
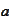 and
and
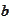 defined via a summation or integration over the variable
defined via a summation or integration over the variable
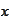 (if there is a possibility of confusion with another variable).
(if there is a possibility of confusion with another variable).
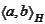 -scalar
product in Hilbert space
-scalar
product in Hilbert space
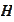 .
.
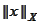 -norm
of
-norm
of
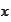 in space
in space
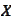 .
.
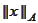 -energy
norm,
-energy
norm,
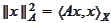 for some
for some
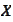 .
.
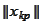 -matrix
with elements
-matrix
with elements
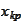 .
.
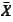 -closure of set
-closure of set
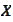 .
.
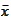 - complex conjugate of number
- complex conjugate of number
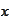 .
.
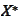 -dual
space of space
-dual
space of space
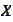 or adjoint operator of operator
or adjoint operator of operator
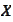 or polar cone to cone
or polar cone to cone
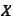 .
.
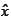 - Fourier or Laplace transform of
- Fourier or Laplace transform of
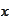 .
.
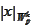 - seminorm consisting of only the highest derivatives, see the section
(
Sobolev spaces
).
- seminorm consisting of only the highest derivatives, see the section
(
Sobolev spaces
).
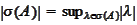 .
.
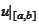 -function
-function
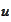 restricted to the interval
restricted to the interval
![$\left[ a,b\right] $](graphics/notesCF__0__60.gif) .
.
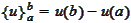 .
.
 .
.
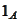 - Indicator of event
- Indicator of event
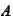 or indicator function of the set
or indicator function of the set
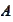 .
It is equal to 1 if the
.
It is equal to 1 if the
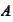 is true
(
is true
(
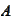 occurs or
occurs or
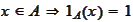 )
and zero otherwise. In particular,
Prob
)
and zero otherwise. In particular,
Prob
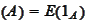 .
.
 -
-
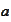 is asymptotically equal to
is asymptotically equal to
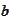 :
:
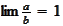 or
or
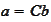 for a constant
for a constant
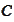 (in Bayesian analysis context) or random variable
(in Bayesian analysis context) or random variable
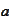 is distributed like
is distributed like
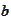 or
or
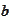 is asymptotic expansion of
is asymptotic expansion of
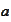 .
.
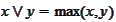 (greater of the two as in "union").
(greater of the two as in "union").
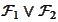 - the minimal
- the minimal
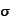 -algebra
containing the union of the set collections
-algebra
containing the union of the set collections
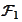 and
and
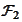 .
.
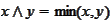 (as in "intersection").
(as in "intersection").
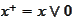 .
.
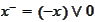 .
.
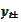 is the limit
is the limit
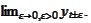
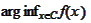 -
the set of points
-
the set of points
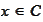 where the
where the
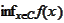 is achieved.
is achieved.
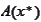 -indexes
of active constraints at the feasible point
-indexes
of active constraints at the feasible point
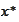 .
.
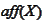 -affine
hull of the set
-affine
hull of the set
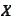 .
.
a.s. - almost surely.
a.e. - almost everywhere.
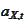 -
drift of the process
-
drift of the process
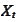 at time
at time
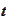 :
:
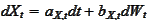 .
.
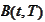 - price of a risky bond with zero recovery as observed at
- price of a risky bond with zero recovery as observed at
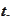 The
The
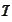 is the maturity of the bond.
is the maturity of the bond.
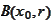 - ball of radius
- ball of radius
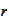 centered at
centered at
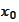 .
.
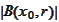 -volume
of the ball.
-volume
of the ball.
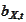 -
(matrix of) volatility of the process
-
(matrix of) volatility of the process
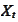 at time
at time
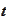 :
:
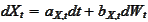 .
.
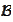 - Borel field on real line.
- Borel field on real line.
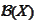 - Borel field over the topological space
- Borel field over the topological space
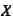 .
.
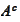 - complement of the set
- complement of the set
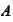 .
.
ch.f. - characteristic function.
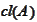 -closure
of
-closure
of
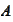 ,
see (
Convex Hull, Cone,
Relative Interior
).
,
see (
Convex Hull, Cone,
Relative Interior
).
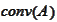 -convex
hull of
-convex
hull of
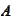 ,
see (
Convex hull
).
,
see (
Convex hull
).
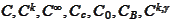 see the section (
Function spaces
section
).
see the section (
Function spaces
section
).
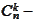 binomial
coefficients,
binomial
coefficients,
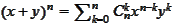 ,
,
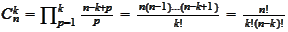 .
.
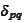 or
or
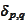 - Kronecker's delta.
- Kronecker's delta.
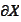 - boundary of the set
- boundary of the set
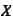 .
.
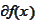 -subdifferential
of the function
-subdifferential
of the function
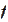 at the point
at the point
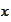 .
.
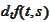 -differential
of the function
-differential
of the function
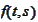 applied to the argument
applied to the argument
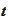 .
.
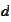 - in finite element, PDE and Sobolev space sections
"
- in finite element, PDE and Sobolev space sections
"
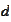 "
refers to diameter of
"
refers to diameter of
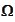 (spacial set under consideration).
(spacial set under consideration).
d.f. - distribution function.
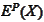 - expectation of
- expectation of
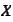 taken with respect to the probability measure
taken with respect to the probability measure
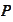 .
.
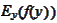 - expectation of
- expectation of
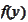 applied to the random quantity
applied to the random quantity
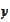 .
.
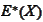 - risk neutral expectation of
- risk neutral expectation of
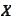 ,
see (
Risk neutral pricing
).
,
see (
Risk neutral pricing
).
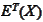 - expectation of
- expectation of
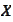 with respect to the
with respect to the
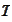 -forward probability measure, see
(
T-forward probability measure
).
-forward probability measure, see
(
T-forward probability measure
).
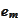 -vector
-vector
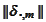 .
.
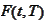 - forward price as observed at
- forward price as observed at
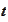 with maturity
with maturity
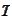 .
.
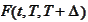 - forward LIBOR observed at
- forward LIBOR observed at
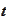 and effective during
and effective during
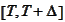 ,
see (
Forward LIBOR
).
,
see (
Forward LIBOR
).
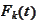 =
=
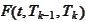 ,
given the settlement dates structure
,
given the settlement dates structure
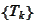 .
.
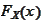 -feasible
direction cone of the set
-feasible
direction cone of the set
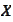 at the point
at the point
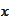 .
.
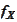 - characteristic function of a random variable
- characteristic function of a random variable
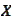 .
.
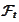 - the
- the
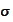 -algebra
containing information available at time
-algebra
containing information available at time
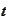 .
.
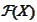 - the
- the
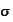 -algebra
generated by the r.v.
-algebra
generated by the r.v.
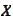 .
.
GMRA - generalized multiresolution analysis.
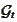 -
-
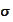 -algebra
containing both (cross product of)
-algebra
containing both (cross product of)
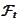 and
and
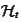 .
.
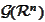 - Schwartz space (see the formula (
Schwartz
space
)).
- Schwartz space (see the formula (
Schwartz
space
)).
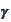 -
chunkiness parameter in finite elements sections, hazard rate in financial
sections.
-
chunkiness parameter in finite elements sections, hazard rate in financial
sections.
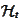 -
-
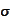 -algebra
generated by credit events or Poisson jumps.
-algebra
generated by credit events or Poisson jumps.
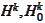 - see the section (
Sobolev spaces
section
).
- see the section (
Sobolev spaces
section
).
iff - if and only if.
iid - independent identically distributed.
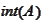 - interior of set
- interior of set
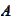 .
.
i.o. - infinitely often.
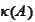 -condition
number of matrix
-condition
number of matrix
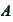 .
.
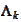 - finite difference approximation of the second derivative at the
- finite difference approximation of the second derivative at the
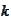 -th
knot of the lattice.
-th
knot of the lattice.
LHS - left hand side (of equation).
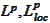 see the section (
Function spaces
section
).
see the section (
Function spaces
section
).
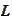 - linear operator, usually differential operator of elliptic type or a
generator of Markov process.
- linear operator, usually differential operator of elliptic type or a
generator of Markov process.
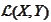 - space of linear bounded operators acting from
- space of linear bounded operators acting from
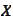 to
to
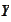 .
.
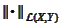 -strong
operator norm from
-strong
operator norm from
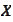 to
to
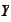 .
.
MRA - multiresolution analysis.
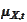 -
geometric drift of the process
-
geometric drift of the process
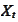 at time
at time
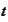 :
:
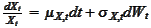 .
.
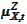 -geometric
drift of the process
-geometric
drift of the process
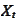 under numeraire
under numeraire
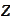 ,
,
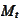 - some martingale.
- some martingale.
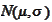 - normal variable with mean
- normal variable with mean
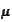 and standard deviation
and standard deviation
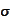 .
.
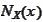 -normal
cone of the set
-normal
cone of the set
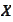 at the point
at the point
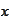 .
.
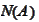 -null
space of matrix or operator
-null
space of matrix or operator
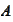 .
.
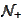 -positive integers,
-positive integers,
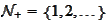 .
.
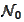 -non-negative integers,
-non-negative integers,
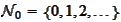 .
.
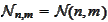 -integer
interval,
-integer
interval,
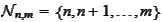 ,
,
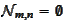 for
for
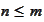 .
.
OST - orthonormal system of translates.
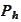 - orthogonal projection on the finite element space
- orthogonal projection on the finite element space
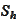 (see the definition (
Orthogonal L2
projection
)).
(see the definition (
Orthogonal L2
projection
)).
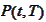 - price of the riskless bond with zero recovery as observed at
- price of the riskless bond with zero recovery as observed at
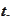 The
The
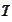 is the maturity of the bond.
is the maturity of the bond.
p.m. - probability measure.
in pr. - in probability. For example,
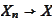 in pr. means
"
in pr. means
"
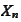 converges to
converges to
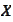 in probability".
in probability".
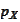 -distribution
of the random variable
-distribution
of the random variable
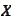 .
.
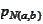 -distribution
of the normal variable
-distribution
of the normal variable
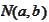 .
.
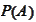 - probability of the event
- probability of the event
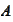 .
.
Prob
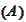 - probability of the event
- probability of the event
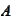 .
.
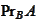 - projection of A on B.
- projection of A on B.
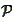 -the
set of all absolutely continuous measures with respect to the measure
-the
set of all absolutely continuous measures with respect to the measure
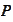 of
of
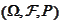 in real variable context or the class of "shape functions" in finite element
context.
in real variable context or the class of "shape functions" in finite element
context.
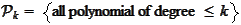 in finite element context.
in finite element context.
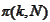 -set
of permutations of
-set
of permutations of
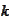 integers taken from the range
integers taken from the range
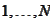 .
.
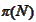 -set
of permutations of
-set
of permutations of
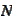 integers taken from the range
integers taken from the range
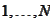 .
.
RHS - right hand side (of equation).
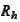 - Ritz projection on finite element space
- Ritz projection on finite element space
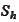 (see the definition (
Elliptic Ritz
projection
)).
(see the definition (
Elliptic Ritz
projection
)).
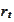 - riskless rate.
- riskless rate.
r.v. - random variable.
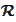 - real line.
- real line.
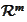 -
-
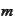 -dimensional
space.
-dimensional
space.
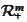 -non-negative
quadrant of the
-non-negative
quadrant of the
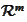 .
.
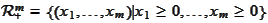 .
.
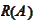 -range
of matrix or operator
-range
of matrix or operator
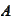 .
.
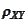 - correlation of quantities
- correlation of quantities
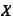 and
and
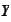 .
.
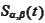 - swap rate for a vanilla fixed-for-floating LIBOR swap with payments
occurring at
- swap rate for a vanilla fixed-for-floating LIBOR swap with payments
occurring at
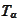 ,...,
,...,
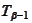 .
.
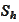 - finite element space.
- finite element space.
span
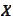 - linear span of the set
- linear span of the set
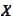 .
.
s.p.m. - subprobability measure.
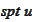 - support set of the function
- support set of the function
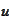 .
.
supp
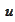 - support set of the function
- support set of the function
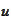 .
.
s.t. - such that.
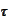 - stopping time or default time.
- stopping time or default time.
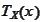 -tangent
cone of the set
-tangent
cone of the set
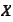 at the point
at the point
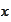 .
.
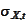 - (column of) geometric volatility of the process
- (column of) geometric volatility of the process
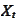 at time
at time
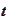 :
:
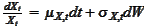 .
.
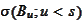 - sigma algebra generated by path of the process
- sigma algebra generated by path of the process
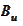 up
to the time
up
to the time
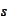 .
.
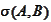 -minimal
sigma algebra containing the components
-minimal
sigma algebra containing the components
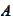 and
and
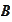 .
.
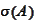 - spectrum of operator
- spectrum of operator
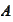 .
.
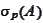 - point spectrum of operator
- point spectrum of operator
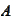 .
.
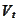 - a value of a derivative at time
- a value of a derivative at time
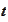 .
.
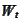 - (column of) standard Brownian motion at
- (column of) standard Brownian motion at
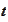 .
.
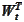 - (column of) standard Brownian motion with respect to the
- (column of) standard Brownian motion with respect to the
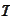 -forward
probability measure.
-forward
probability measure.
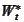 - (column of) standard Brownian motion with respect to the risk neutral
probability measure.
- (column of) standard Brownian motion with respect to the risk neutral
probability measure.
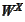 -
(column of) standard Brownian motion with respect to the numeraire
-
(column of) standard Brownian motion with respect to the numeraire
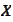 .
.
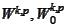 - see the section (
Sobolev spaces
section
).
- see the section (
Sobolev spaces
section
).
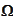 - event space (complete description of what may happen).
- event space (complete description of what may happen).
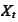
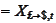 - spot dollar price of a pound.
- spot dollar price of a pound.
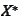 -dual
space if
-dual
space if
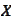 is a space with linearity and topology, polar cone if
is a space with linearity and topology, polar cone if
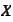 is a cone, conjugate operator or matrix if
is a cone, conjugate operator or matrix if
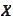 is an operator or a matrix, convex conjugate function if
is an operator or a matrix, convex conjugate function if
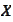 is a function.
is a function.
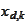 or
or
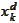 - mesh in the chapters on wavelets and finite elements.
- mesh in the chapters on wavelets and finite elements.
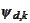 or
or
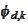 - scale and transport operations applied to functions
- scale and transport operations applied to functions
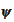 or
or
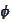 (wavelet chapter).
(wavelet chapter).
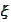 - standard normal variable.
- standard normal variable.
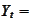
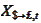 ,
spot pound price of a dollar.
,
spot pound price of a dollar.
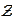 - set of all integers,
- set of all integers,
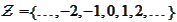 .
.
|