his section lists some common notations.
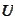is an open subset of
.
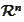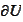is the boundary of
.
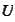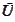is the closure of
.
.
.
.
.
.
.
.
.
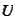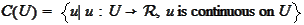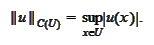
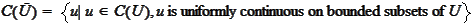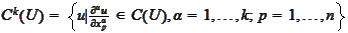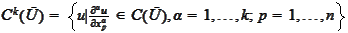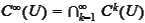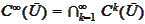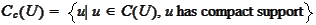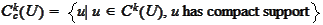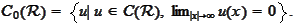
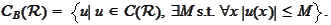
For a function
we
denote
|
|
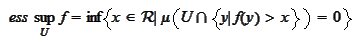
(ess sup definition)
|
where the
is the Lebesgue measure (see the proposition
(
Existence of Lebesgue
measure
)).
,
.
,
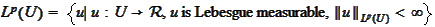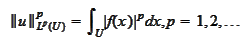
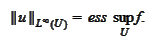
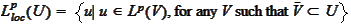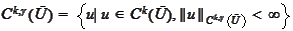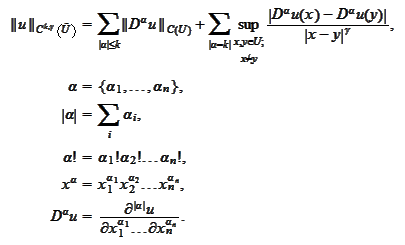
is the "Schwartz space" of infinitely differentiable functions
such
that for any polynomial
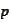of finite dimension and any multi-index
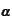we
have
|
|
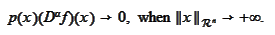
(Schwartz space)
|
|
