et
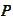 be a probability measure,
be a probability measure,
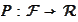 for a
for a
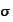 -algebra
-algebra
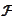 .
An
.
An
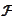 -measurable
random variable
-measurable
random variable
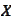 :
:
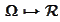 gives rise to the set function
gives rise to the set function
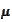 given by the
relationship
given by the
relationship
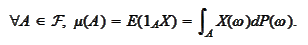 The measure
The measure
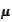 does not have to be positive or normalized to 1. This brings us to
consideration of a wider class of measures.
does not have to be positive or normalized to 1. This brings us to
consideration of a wider class of measures.
Proof
Using the notation of the previous proposition set
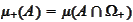 and
and
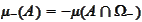 .
.
Definition
The measure
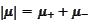 is called "total variation" or "absolute value" of
is called "total variation" or "absolute value" of
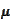 .
.
|