et
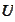 be an open bounded subset of
be an open bounded subset of
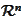 .
The
.
The
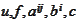 are
functions
are
functions
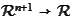 .
The
.
The
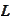 is a linear differential
operator
is a linear differential
operator
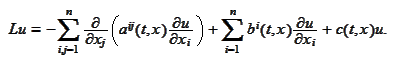
|
|
(Operator L)
|
Problem
(Elliptic Dirichlet
problem).
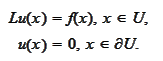
Let us multiply the equations of the problem
(
Elliptic Dirichlet problem
) with a
function
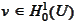 and integrate with respect to
and integrate with respect to
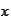 over
over
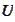 .
After integration by parts we
obtain
.
After integration by parts we
obtain
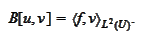
Definition
(Weak solution of
elliptic Dirichlet problem). The function
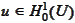 is a "weak solution" of the problem
(
Elliptic Dirichlet problem
) if it
satisfies
is a "weak solution" of the problem
(
Elliptic Dirichlet problem
) if it
satisfies
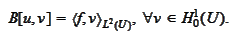
|