e consider the sequence of r.v.
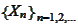 and a triple
and a triple
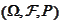 .
The
.
The
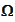 is the event space of
is the event space of
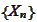 and
and
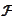 is the minimal
is the minimal
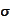 -algebra
that makes all
-algebra
that makes all
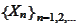 measurable. We think of
measurable. We think of
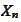 as a consecutive sequence of trials as
as a consecutive sequence of trials as
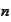 increases. Hence,
increases. Hence,
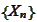 is a "process" and
is a "process" and
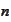 is a time parameter.
is a time parameter.
We use the notation
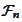 to represent the
to represent the
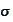 -algebra
containing the information available up to time
-algebra
containing the information available up to time
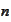 .
Hence,
.
Hence,
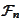 is the minimal
is the minimal
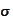 -algebra
that makes the family
-algebra
that makes the family
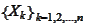 measurable.
measurable.
We use the notation
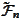 to represent the
to represent the
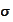 -algebra
containing the information that comes after the time
-algebra
containing the information that comes after the time
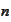 .
Hence,
.
Hence,
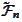 is the minimal
is the minimal
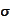 -algebra
that makes the the family
-algebra
that makes the the family
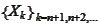 measurable.
measurable.
We use the notation
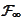 to represent the minimal
to represent the minimal
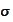 -algebra
that contains all of the
-algebra
that contains all of the
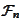 ,
,
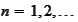 .
By the minimality of
.
By the minimality of
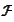 we have
we have
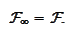
We use the notation
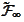 for the intersection
for the intersection
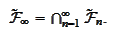
|
|
(Remote field)
|
Sometimes it is convenient to think of
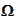 as
the product
space
as
the product
space
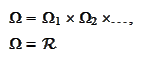
|
|
(Random walk space)
|
where each
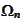 is the probability space for
is the probability space for
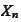 .
The
.
The
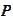 is the product measure consistent with the d.f.
is the product measure consistent with the d.f.
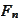 on each
on each
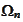 .
The
.
The
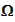 is a collection of infinite sequences of real
numbers:
is a collection of infinite sequences of real
numbers:
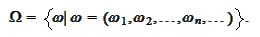 The
The
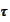 denotes the
"shift":
denotes the
"shift":
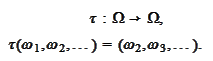
|
|
(Shift)
|
The
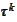 is the
is the
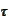 applied
applied
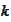 times.
times.
The
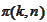 denotes the set of permutations of
denotes the set of permutations of
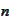 integers from the range
integers from the range
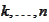 .
A permutation
.
A permutation
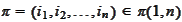 (and similarly
(and similarly
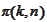 )
produces a mapping on
)
produces a mapping on
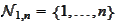 and on
and on
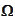 according to the
rules
according to the
rules
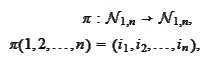
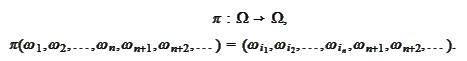
|
|
(Permutation)
|
Definition
(Invariant set) The set
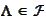 is called "invariant" if
is called "invariant" if
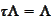 .
.
Definition
(Remote event). Any set
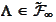 (see the formula (
Remote field
)) is called
"remote event".
(see the formula (
Remote field
)) is called
"remote event".
Clearly, an invariant set is remote and a remote set is permutable.
|