ccording to the proposition
(
Infinitely often zero-or-one
law
), for a random walk
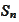
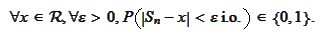
Proposition
(Structure of recurrent values) The
set
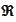 is described by one of the following statements.
is described by one of the following statements.
1.
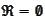 .
.
2.
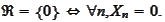
3.
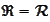 .
.
4.
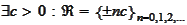 .
.
Note that
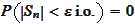 means
means
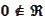 and
and
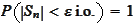 means
means
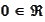 .
.
Proof
The statement 1 is a direct consequence of the proposition
(
Borel-Cantelli lemma, part
1
). The statement 2 does not follow from
(
Borel-Cantelli lemma, part
2
) because
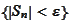 are not independent events. Hence, we proceed with the proof of 2.
are not independent events. Hence, we proceed with the proof of 2.
By the definition (
Limsup and liminf
for sets
), for a family of sets
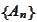
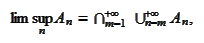 then
then
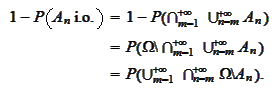 Thus, for any
Thus, for any
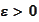 ,
,
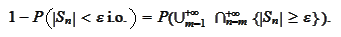 According to the section
(
Operations on sets and
logical statements
), the statement
According to the section
(
Operations on sets and
logical statements
), the statement
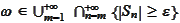 means
means
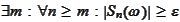 .
Therefore, we
continue
.
Therefore, we
continue
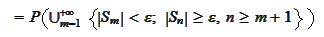 The above statements within the union are disjoint:
The above statements within the union are disjoint:
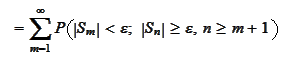 Note that
Note that
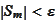 and
and
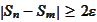 imply
imply
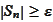 .
Hence,
.
Hence,
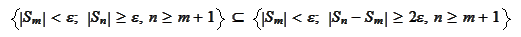 and the events
and the events
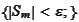 and
and
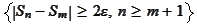 are
independent:
are
independent:
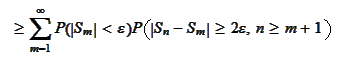 Note that
Note that
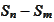 is distributed as
is distributed as
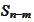 :
:
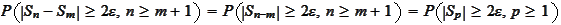 .
Hence, the second probability is
.
Hence, the second probability is
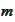 -independent:
-independent:
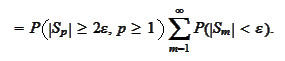 If follows that if
If follows that if
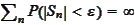 then we must have
then we must have
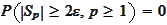 .
.
Next, we complete the proof by showing that
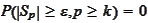 for any
for any
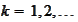 .
We introduce the
event
.
We introduce the
event
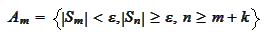 and note that the
events
and note that the
events
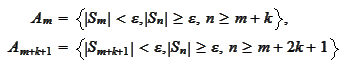 are disjoint. Hence, we
have
are disjoint. Hence, we
have
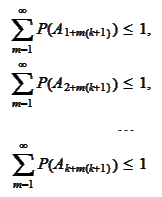 and,
consequently,
and,
consequently,
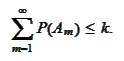 We now repeat the argument that lead to
We now repeat the argument that lead to
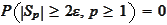 starting from
starting from
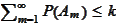 .
.
Proposition
(Recurrence result 1) If
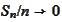 in pr. then
in pr. then
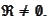
|