The
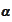 points out some time index and does so based on the information about the path
of the process up to that time index. For a particular path
points out some time index and does so based on the information about the path
of the process up to that time index. For a particular path
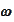 one can have
one can have
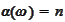 for at most one
index:
for at most one
index:
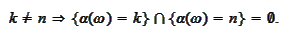 For these reasons the
For these reasons the
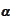 is sometimes called "stopping time".
is sometimes called "stopping time".
The
pre-
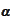 field is a collection of scenarios that lead to the optional event
field is a collection of scenarios that lead to the optional event
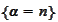 .
In
particular,
.
In
particular,
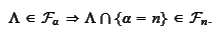
Thus, for every
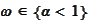 the time
the time
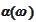 is defined and then
is defined and then
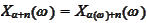 for
for
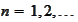 .
In other words,
.
In other words,
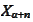 is the part of the path
is the part of the path
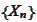 after the stopping time
after the stopping time
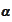 with the
pre-
with the
pre-
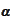 part shifted forward and
away:
part shifted forward and
away:
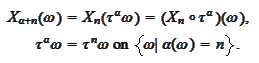
Assuming the representation of the formula
(
Random walk space
),
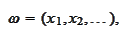
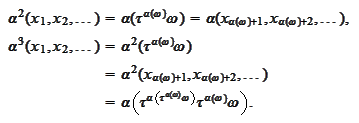 In other words,
In other words,
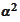 is the stopping time calculated from the path
is the stopping time calculated from the path
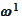 obtained by shifting forward the original path
obtained by shifting forward the original path
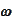 by
by
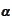 calculated on
calculated on
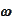 :
:
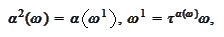 and we
continue
and we
continue
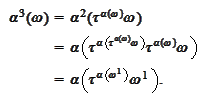 The
The
 is the path obtained by shifting forward
is the path obtained by shifting forward
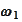 by the
by the
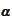 calculated on
calculated on
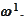 We call it
We call it
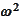 :
:
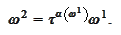 Hence, we obtain another way to understand
Hence, we obtain another way to understand
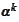 and
and
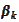 .
.
Proposition
(Maximum of random walk) Let
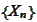 be a stationary independent process,
be a stationary independent process,
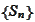 is the associated random walk and the r.v.
is the associated random walk and the r.v.
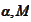 are defined
by
are defined
by
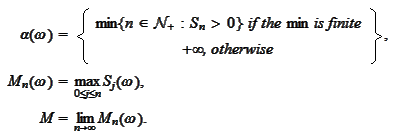 Then the statements A,B,C are equivalent and the statements a,b,c are
equivalent.
Then the statements A,B,C are equivalent and the statements a,b,c are
equivalent.
A.
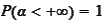 .
.
B.
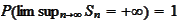 .
.
C.
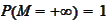 .
.
a.
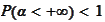 .
.
b.
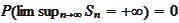 .
.
c.
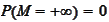 .
.
Proof
Note that the events
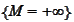 and
and
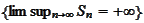 are permutable events. Therefore, according to the proposition
(
Hewitt and Savage zero-or-one
law
) the values 1,0 are the only possible values for
are permutable events. Therefore, according to the proposition
(
Hewitt and Savage zero-or-one
law
) the values 1,0 are the only possible values for
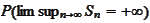 and
and
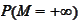 .
Hence, if we prove equivalence of A,B,C then we also obtain equivalence of
a,b,c.
.
Hence, if we prove equivalence of A,B,C then we also obtain equivalence of
a,b,c.
We prove
 as follows. According to the proposition
(
BetaK separation of random
walk
), the variables
as follows. According to the proposition
(
BetaK separation of random
walk
), the variables
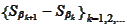 are iid. Hence, the proposition
(
Strong law of large
numbers for iid r.v.
) applies and we
derive
are iid. Hence, the proposition
(
Strong law of large
numbers for iid r.v.
) applies and we
derive
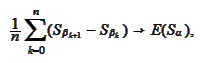 where
where
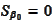 .
We also
have
.
We also
have
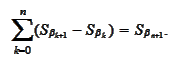 Hence,
Hence,
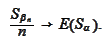 Also,
Also,
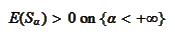 thus
thus
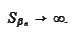 This implies B.
This implies B.
By definition of
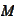 ,
,
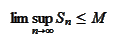 hence, B implies C. The C implies A by definitions of
hence, B implies C. The C implies A by definitions of
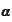 and
and
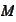 .
.
Proposition
(Eventuality of random walk) Let
 be a stationary independent process and
be a stationary independent process and
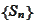 is the associated random walk. There are only four mutually exclusive
possibilities, each taking place a.s.
is the associated random walk. There are only four mutually exclusive
possibilities, each taking place a.s.
1.
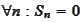 ,
,
2.
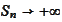 ,
,
3.
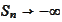 ,
,
4.
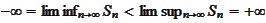 .
.
|