et
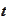 be observation time. We consider an agreement to invest at time
be observation time. We consider an agreement to invest at time
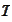 ,
,
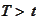 ,
a fixed amount of cash and collect at
,
a fixed amount of cash and collect at
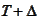 ,
,
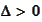 ,
one unit of reference currency. We denote
,
one unit of reference currency. We denote
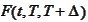 the simple compounding rate during the time interval
the simple compounding rate during the time interval
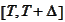 implied by such a contract. We replicate this contract by selling
implied by such a contract. We replicate this contract by selling
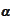 units of bond
units of bond
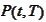 and purchasing one unit of bond
and purchasing one unit of bond
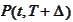 .
If the implied rate
.
If the implied rate
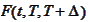 is fair then the contract should not worth anything at time
is fair then the contract should not worth anything at time
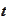 :
:
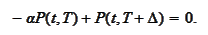 The cash flow at time
The cash flow at time
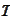 is
is
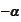 .
According to the contract, the investment will grow at the rate
.
According to the contract, the investment will grow at the rate
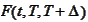 up to the time
up to the time
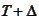 when it pays 1 unit of currency.
Therefore
when it pays 1 unit of currency.
Therefore
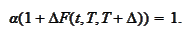 We conclude that the fair rate for the contract is given by the
relationship
We conclude that the fair rate for the contract is given by the
relationship
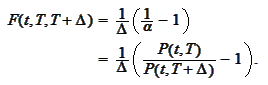
|
|
(Libor)
|
By definition, this is the "forward LIBOR". The structure of the last formula
is such that the rate
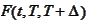 is a
is a
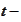 martingale
with respect to the
martingale
with respect to the
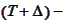 forward
probability measure
Prob
forward
probability measure
Prob
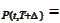 Prob
Prob
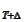 .
.
|