anilla swap agreement has positive cashflows at times
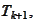
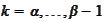calculated as
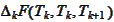and negative cashflows at times
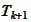calculated as
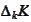where
.
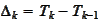The number
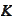is some predetermined fixed rate. The swap rate
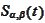is the particular value of the parameter
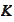that makes such contract of zero value at the time
.
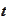Hence, the
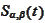is defined by the
relationship
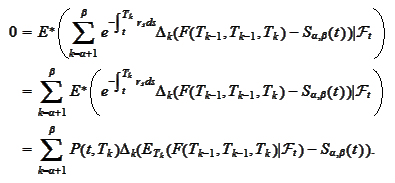Since
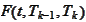is a martingale with respect to the
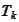-forward
measure we
continue
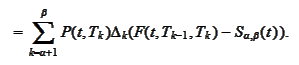Hence,
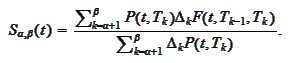Observe
that
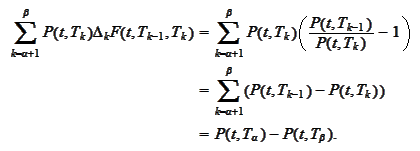Therefore,
|
|
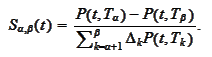
(Swap rate)
|
It is useful to express price of swap with any parameter
through the swap rate. Similarly to the above computations we
have
|
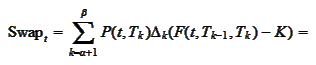
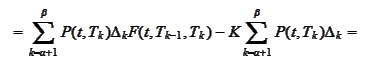
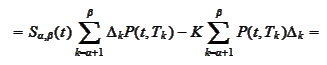
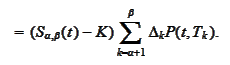
