he
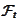 is a reference filtration and
is a reference filtration and
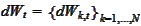 is a column of
is a column of
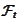 -adapted
independent standard Brownian motions. Consider a column of prices of several
traded assets
-adapted
independent standard Brownian motions. Consider a column of prices of several
traded assets
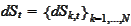 :
:
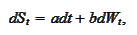 where
where
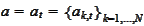 and
and
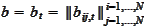 are column and matrix-valued processes adapted to the filtration
are column and matrix-valued processes adapted to the filtration
 .
For simplicity we restrict our attention to assets without dividends. We
assume a possibility to construct a portfolio
.
For simplicity we restrict our attention to assets without dividends. We
assume a possibility to construct a portfolio
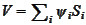 such that the value of the portfolio is deterministic during the next
infinitesimally small time
interval:
such that the value of the portfolio is deterministic during the next
infinitesimally small time
interval:
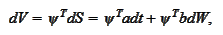
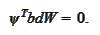 The
The
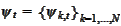 is another column-valued process adapted to
is another column-valued process adapted to
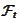 .
It represents trading strategy. By no-arbitrage assumption we conclude that
such riskless portfolio must earn the riskless rate
.
It represents trading strategy. By no-arbitrage assumption we conclude that
such riskless portfolio must earn the riskless rate
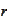 :
:
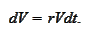 Equivalently,
Equivalently,
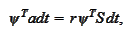 where the
where the
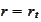 is stochastic
is stochastic
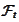 -adapted
riskless rate. We summarize the above argument with the following
statement
-adapted
riskless rate. We summarize the above argument with the following
statement
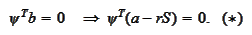 We think of columns
We think of columns
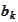 ,
,
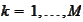 of the matrix
of the matrix
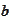 as elements of a linear space of some finite dimension. We introduce the
linear span
as elements of a linear space of some finite dimension. We introduce the
linear span
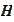 of the set
of the set
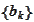 .
Let
.
Let
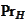 be an orthogonal projection to the linear span
be an orthogonal projection to the linear span
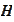 .
The statement (*) reads as
.
The statement (*) reads as
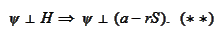 We would like to conclude that
We would like to conclude that
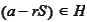 .
Indeed, suppose such conclusion is false and there is a nonzero element
.
Indeed, suppose such conclusion is false and there is a nonzero element
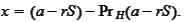 We
have
We
have
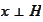 by the form of the
by the form of the
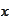 .
We arrive to a contradiction by taking
.
We arrive to a contradiction by taking
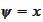 in the statement (**). Therefore
in the statement (**). Therefore
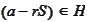 .
Equivalently, there are
.
Equivalently, there are
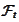 -adapted
processes
-adapted
processes
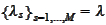 such that
such that
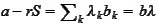 or
or
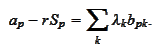
|
|
(Market price of risk)
|
This result is remarkable because the
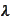 is dependent only on one index. The formula
(
Market_price_of_risk
) states that the
excess return of the asset over the riskless rate
is dependent only on one index. The formula
(
Market_price_of_risk
) states that the
excess return of the asset over the riskless rate
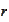 is proportional to the volatilities associated with the driving Brownian
motions
is proportional to the volatilities associated with the driving Brownian
motions
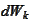 and the coefficient of proportionality
and the coefficient of proportionality
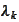 does not depend on the type of the asset but is only dependent on the source
of risk. Therefore, the coefficients
does not depend on the type of the asset but is only dependent on the source
of risk. Therefore, the coefficients
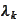 are
called "market prices of risk". We
have
are
called "market prices of risk". We
have
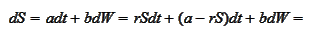
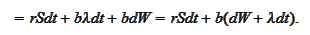
|
|
(Risk neutral Brownian motion)
|
According to the proposition (
Girsanov
theorem
), there exists a change of the probability measure that makes the
process
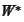 given by
given by
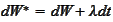 a standard Brownian motion. Such probability measure is called "the risk
neutral measure". Note that
a standard Brownian motion. Such probability measure is called "the risk
neutral measure". Note that
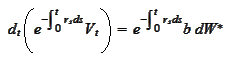 hence the discounted price of any traded asset
hence the discounted price of any traded asset
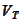 is a martingale with respect to the risk neutral measure
:
is a martingale with respect to the risk neutral measure
:
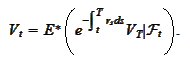
|
|
(Risk neutral pricing)
|
The above relation is the foundation of classic derivative pricing.
Consider the following special
situation:
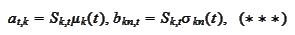 where the
where the
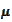 and
and
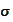 are some deterministic functions of time. The
(
Market price of risk
) reads
as
are some deterministic functions of time. The
(
Market price of risk
) reads
as
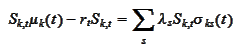 or
or
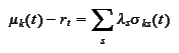
Hence, in the setting (***), if
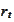 is a deterministic function then the market prices of risk are deterministic
functions as well.
is a deterministic function then the market prices of risk are deterministic
functions as well.
A particular vector
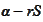 may be represented as a linear combination of
may be represented as a linear combination of
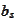 in many different ways if the number of vectors
in many different ways if the number of vectors
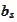 is bigger then the dimensionality of their linear span. If there are more
sources of uncertainty than traded assets then the risk neutral measure is not
unique. This means that there may be a variety of opinions about prices of
contingent claims but still there is no arbitrage.
is bigger then the dimensionality of their linear span. If there are more
sources of uncertainty than traded assets then the risk neutral measure is not
unique. This means that there may be a variety of opinions about prices of
contingent claims but still there is no arbitrage.
|