e follow the setup of the two previous sections
(
Girsanov setup
) and
(
Girsanov change of measure
) but give the
direct derivation of the expression for the changed probability measure. We
consider a "small time interval" version of the formula
(
Change of measure
):
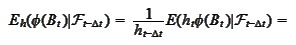 The last formula is the equation that we need to satisfy by selecting a
process
The last formula is the equation that we need to satisfy by selecting a
process
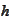 .
The
.
The
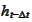 ,
,
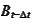 ,
,
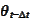 are deterministic functions from point of view of
are deterministic functions from point of view of
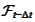 .
The
.
The
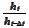 and
and
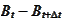 are random variables from the point of view of
are random variables from the point of view of
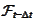 .
These variables represent a small change over the time interval
.
These variables represent a small change over the time interval
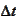 .
The distribution of
.
The distribution of
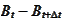 is known,
is known,
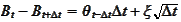 for a column of iid standard normal variables
for a column of iid standard normal variables
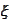 in the "original measure". The distribution of
in the "original measure". The distribution of
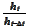 is what we are trying to find from the above equation. We seek
is what we are trying to find from the above equation. We seek
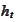 as
a variable adapted to the filtration generated by
as
a variable adapted to the filtration generated by
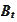 .
Hence, we express the last "original measure" expectation as follows
.
Hence, we express the last "original measure" expectation as follows
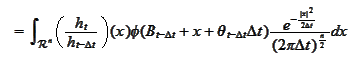 where
where
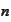 is dimensionality of
is dimensionality of
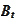 .
In the last integral the
.
In the last integral the
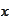 is the integration parameter over all possible values of
is the integration parameter over all possible values of
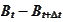 and
and
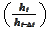 is a function of
is a function of
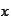 because
because
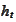 is
is
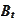 -adapted.
-adapted.
The last integral is supposed to be equal to
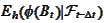 for any smooth and sharply decaying function
for any smooth and sharply decaying function
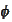 .
We seek
.
We seek
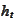 such that the
such that the
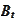 would be a standard Brownian motion in the new (changed) measure:
would be a standard Brownian motion in the new (changed) measure:
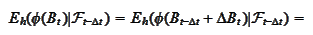
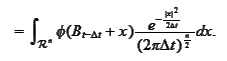 We need the former and the latter integrals to be equal. This gives us a
recipe for construction of the
We need the former and the latter integrals to be equal. This gives us a
recipe for construction of the
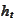 .
.
We introduce the convenience notation
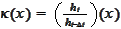 and
and
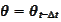 and state that we are seeking a
and state that we are seeking a
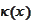 satisfying
satisfying
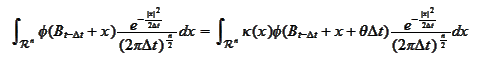 for any smooth
for any smooth
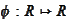 .
To make conclusions we need to have the same expression as an argument of
.
To make conclusions we need to have the same expression as an argument of
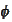 .
Hence, we make a change of variable
.
Hence, we make a change of variable
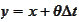 in the right integral. It
becomes
in the right integral. It
becomes
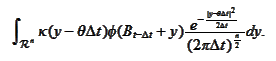 Therefore,
Therefore,
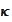 has to
satisfy
has to
satisfy
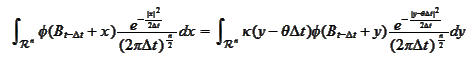 for any smooth
for any smooth
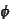 .
Hence,
.
Hence,
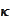 must
satisfy
must
satisfy
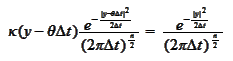 or
or
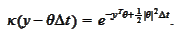 Changing to the original variable
Changing to the original variable
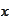 we
obtain
we
obtain
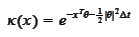 or, in the original
notation,
or, in the original
notation,
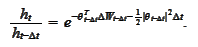 Using the above SDE and the boundary condition
Using the above SDE and the boundary condition
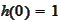 we
conclude
we
conclude
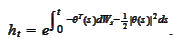
|
|
(Girsanov kernel)
|
We summarize with the following statement.
|