We
are given a probability space
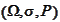 (see the section
(
Definition of
conditional probability
)) and a filtration
(see the section
(
Definition of
conditional probability
)) and a filtration
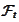 (see the section (
Filtration
definition
)). Let
(see the section (
Filtration
definition
)). Let
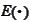 be the expectation associated with the measure
be the expectation associated with the measure
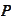 .
We introduce another
expectation
.
We introduce another
expectation
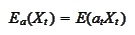
|
|
(Definition of change of measure)
|
defined for any
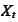 and a particular
and a particular
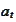 ,
where
,
where
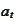 and
and
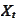 are continuous processes adapted to the filtration
are continuous processes adapted to the filtration
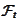 and
and
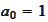 .
The Girsanov's theorem (
Girsanov_theorem
)
hints that
.
The Girsanov's theorem (
Girsanov_theorem
)
hints that
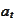 should be a positive martingale.
should be a positive martingale.
We would like to calculate
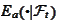 in terms of
in terms of
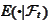 .
We noted in the section (
Filtration
and conditional expectation
) that the formula
(
Chain rule
) may regarded as a definition of
conditional probability. Hence, we
require
.
We noted in the section (
Filtration
and conditional expectation
) that the formula
(
Chain rule
) may regarded as a definition of
conditional probability. Hence, we
require
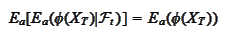 for any smooth function
for any smooth function
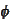 .
Because
.
Because
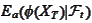 is an
is an
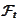 -adapted
random variable, we apply the formula
(
Definition_of_change_of_measure
)
on the left-hand
side:
-adapted
random variable, we apply the formula
(
Definition_of_change_of_measure
)
on the left-hand
side:
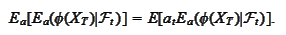 On the right-hand side we apply the formula
(
Definition_of_change_of_measure
)
directly
On the right-hand side we apply the formula
(
Definition_of_change_of_measure
)
directly
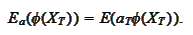 Hence,
Hence,
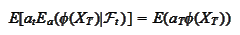 The operation
The operation
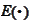 is the original measure, hence, the formula
(
Chain_rule
) holds and the last expression is
is the original measure, hence, the formula
(
Chain_rule
) holds and the last expression is
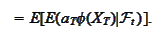 Left and right sides are equal:
Left and right sides are equal:
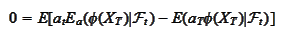 for any
for any
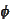 .
We
conclude
.
We
conclude
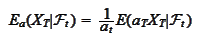
|
|
(Main property of change of measure)
|
for
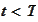 .
The proof of the last step is a standard analysis argument. We express the
expectations in terms of integrals with respect to the corresponding
distributions. If there is a point where the desired property is untrue then
we take a sequence of
.
The proof of the last step is a standard analysis argument. We express the
expectations in terms of integrals with respect to the corresponding
distributions. If there is a point where the desired property is untrue then
we take a sequence of
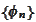 converging to the delta function around such point and obtain a contradiction.
converging to the delta function around such point and obtain a contradiction.
|