The operation
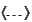 extends
to all Ito processes through the linearity in both
arguments:
extends
to all Ito processes through the linearity in both
arguments:
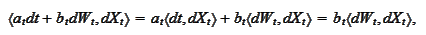
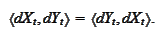
Suppose
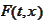 is a smooth function of its arguments. The Ito formula
states
is a smooth function of its arguments. The Ito formula
states
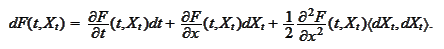
|
|
(Ito formula)
|
The Ito formula is a direct consequence of the Taylor formula
and the considerations of the previous section. Indeed, we are always
interested in the representation of the difference
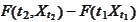 in terms of the infinitesimal
increments:
in terms of the infinitesimal
increments:
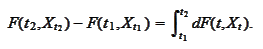 Hence, we apply the Taylor formula to the
Hence, we apply the Taylor formula to the
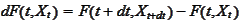 and keep the leading terms.
and keep the leading terms.
 The term
The term
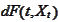 is intended to be used under integral sign. The terms
is intended to be used under integral sign. The terms
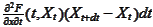 and
and
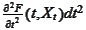 vanish when we take the integral (pass to the dt=0 limit and take a sum) but
the term
vanish when we take the integral (pass to the dt=0 limit and take a sum) but
the term
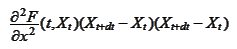 does not vanish by the formula (
Ito isometry
).
This test of survival under the limit dt=0 and sum determines the rules
(
Ito calculus
) at the beginning of this section.
does not vanish by the formula (
Ito isometry
).
This test of survival under the limit dt=0 and sum determines the rules
(
Ito calculus
) at the beginning of this section.
For several variables
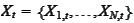 the Ito formula takes
form
the Ito formula takes
form
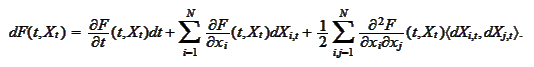
|
|
(Ito formula 2)
|
The following is an important consequence of the Ito
formula:
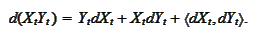
|
|
(Ito derivative of product)
|
To see this consider a linear combination of
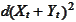 ,
,
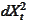 and
and
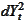 .
.
|