n this section we
are repeatedly using the formulas (
Chain rule
) and
(
Ito_formula
) without further reference. The
filtration is generated by
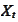 .
The reference is
[Kohn]
.
.
The reference is
[Kohn]
.
A one-dimensional process
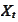 is given by SDE
is given by SDE
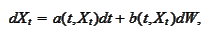 for some smooth functions
for some smooth functions
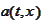 and
and
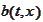 and standard Brownian motion
and standard Brownian motion
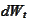 .
.
Let
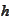 be an integrable function
be an integrable function
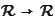 .
.
Proposition
(Backward Kolmogorov for
running payoff) The
function
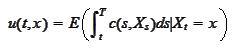 is a solution of the
problem
is a solution of the
problem
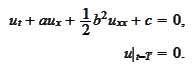
|
|
(Backward Kolmogorov with running payoff)
|
Proposition
(Backward Kolmogorov for
discounted payoff) The function
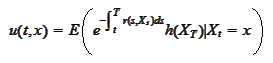 is a solution of the
problem
is a solution of the
problem
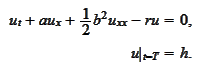
Proof
The proof was already given for the situation when
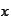 is away from the boundary. On the boundary the statement is obvious.
is away from the boundary. On the boundary the statement is obvious.
|