e are
considering development of some market model during a time interval
![$[0,T].$](graphics/notesCF__0__466.gif) At the time
At the time
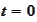 we know nothing about the future and we represent this fact with the trivial
algebra
we know nothing about the future and we represent this fact with the trivial
algebra
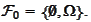 The
The
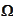 is the event space. It is the full description of what may happen in the
model. By the time moment
is the event space. It is the full description of what may happen in the
model. By the time moment
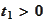 random variables of the model have certain realizations. One may make
particular statements about such realizations that are perfectly verifiable
from the point of view of information available at time
random variables of the model have certain realizations. One may make
particular statements about such realizations that are perfectly verifiable
from the point of view of information available at time
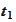 .
Such statements are represented by subsets of
.
Such statements are represented by subsets of
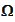 and constitute an algebra
and constitute an algebra
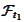 ,
(see section (
Operations on sets
)
for explanation of the "algebra" term in this context). Similarly, for a time
moment
,
(see section (
Operations on sets
)
for explanation of the "algebra" term in this context). Similarly, for a time
moment
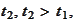 we form an algebra
we form an algebra
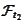 .
Since market participants do not forget information,
.
Since market participants do not forget information,
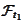 is a subset of
is a subset of
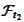 .
A family of such algebras
.
A family of such algebras
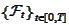 is called "filtration" or "flow of information".
is called "filtration" or "flow of information".
Example
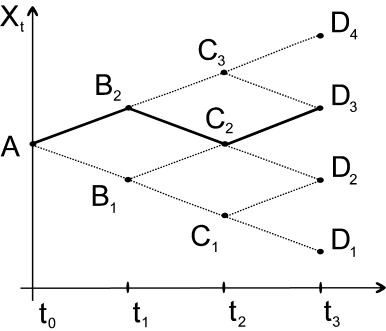
Consider a discrete random walk
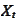 described by the picture. The process
described by the picture. The process
 starts at the point A at time
starts at the point A at time
 .
By the time
.
By the time
 the process may be observed at point
the process may be observed at point
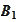 or
or
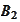 .
Such outcome is uncertain and these are all possibilities at the time
.
Such outcome is uncertain and these are all possibilities at the time
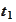 .
Similarly, if the process is at point
.
Similarly, if the process is at point
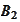 then it may jump up to
then it may jump up to
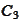 or down to
or down to
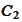 .
.
We introduce the
notation
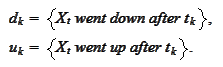 The highlighted path then is described by the elementary random event
The highlighted path then is described by the elementary random event
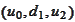 .
At the initial time moment
.
At the initial time moment
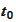 our knowledge is given by the trivial algebra
our knowledge is given by the trivial algebra
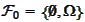 with
with
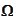 being enumeration of everything that may
happen:
being enumeration of everything that may
happen:
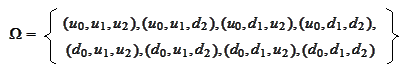 and
and
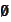 being the event that never happens. At the time
being the event that never happens. At the time
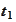 we know where the process went at
we know where the process went at
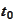 .
Hence,
.
Hence,
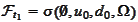 where the
where the
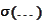 means "take all intersections, unions and complements of the arguments and put
them together into the algebra
means "take all intersections, unions and complements of the arguments and put
them together into the algebra
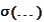 ".
For example,
".
For example,
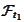 contains the set
contains the set
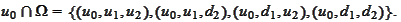 The information at
The information at
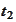 is represented by the algebra
is represented by the algebra
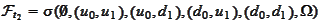 .
For example,
.
For example,
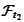 contains the set
contains the set
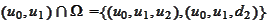 .
The information at
.
The information at
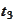 is represented by the algebra
is represented by the algebra
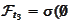 ,
,
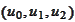 ,
,
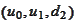 ,
,
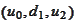 ,
,
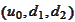 ,
,
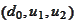 ,
,
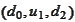 ,
,
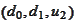 ,
,
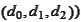 .
.
By definition, a process
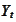 is adapted to a filtration
is adapted to a filtration
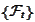 if for any particular
if for any particular
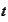 the
the
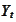 is
is
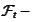 measurable.
Equivalently,
measurable.
Equivalently,
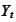 is adapted to
is adapted to
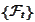 if for any
if for any
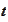 the algebra
the algebra
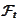 contains the full description of the path
contains the full description of the path
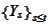 for all times up to
for all times up to
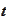 .
For a particular process
.
For a particular process
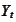 one may form a family
one may form a family
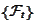 such that for any
such that for any
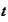 the algebra
the algebra
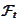 is the minimal algebra that makes the random variable
is the minimal algebra that makes the random variable
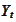
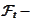 measurable
(for any
measurable
(for any
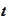 the
the
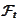 is the minimal description of all possible realizations of
is the minimal description of all possible realizations of
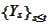 ).
Such a family
).
Such a family
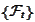 is called "the filtration generated by the
is called "the filtration generated by the
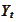 ".
The notation
".
The notation
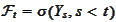 is commonly used to describe the generated filtration.
is commonly used to describe the generated filtration.
Suppose
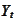 is adapted to
is adapted to
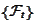 and
and
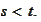 The
The
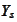 is
is
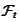 -measurable
(because
-measurable
(because
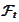 is sufficient to describe
is sufficient to describe
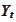 ,
hence, it contains description of
,
hence, it contains description of
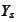 as well). Regularly (unless
as well). Regularly (unless
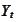 is deterministic during
is deterministic during
![$(s,t]$](graphics/notesCF__0__550.gif) ),
),
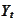 is not
is not
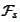 -measurable
because
-measurable
because
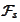 is lacking structure to describe
is lacking structure to describe
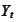 .
However, we may create a crude adjustment of
.
However, we may create a crude adjustment of
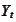 to
to
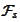 by taking the conditional expectation
by taking the conditional expectation
 for every set
for every set
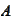 from
from
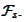 This creates a mapping from
This creates a mapping from
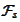 to the range of
to the range of
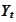 .
A proper restriction of such mapping is an
.
A proper restriction of such mapping is an
 measurable
random variable that we denote
measurable
random variable that we denote
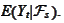 The same (in "almost sure" sense) object
The same (in "almost sure" sense) object
 could be introduced by requiring that the variable
could be introduced by requiring that the variable
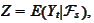 by definition, would be
by definition, would be
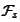 -measurable
and satisfy
-measurable
and satisfy
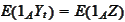 for any set
for any set
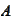 from
from
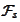 .
.
The
condition
 written in the
form
written in the
form
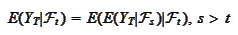
|
|
(Chain rule)
|
is called "the chain rule".
We will say that the random variable
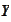 is independent from
is independent from
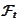 if for any smooth function
if for any smooth function
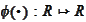 we have
we have
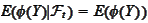 .
.
A random variable
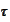 is called the
is called the
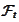 -stopping
time if for any
-stopping
time if for any
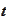 the random event
the random event
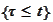 belongs to the
belongs to the
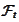 .
In other words,
.
In other words,
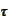 is a stopping time if at any moment
is a stopping time if at any moment
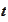 we are able to tell with certainty which of the statements
we are able to tell with certainty which of the statements
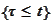 and
and
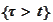 is true.
is true.
|