here are
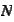 people in the room. What is the probability that at least two of them have the
same birthday?
people in the room. What is the probability that at least two of them have the
same birthday?
Set
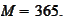 We are interested in
We are interested in
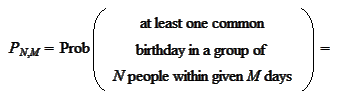 we fix a person
A,
we fix a person
A,
 by the formula (
Bayes
formula
)
by the formula (
Bayes
formula
)

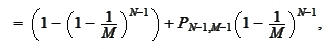
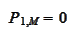 where
where
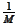 is the probability that a particular person has the same birthday as A,
is the probability that a particular person has the same birthday as A,
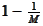 is the probability that a particular person does not have the same birthday as
A,
is the probability that a particular person does not have the same birthday as
A,
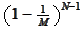 is the probability that in a group of
is the probability that in a group of
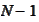 randomly selected individuals no one has the same birthday as A and
randomly selected individuals no one has the same birthday as A and
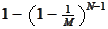 is the probability that in a group of
is the probability that in a group of
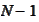 randomly selected individuals someone has the same birthday as A.
randomly selected individuals someone has the same birthday as A.
|