et
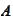and
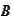be two events of the same event space
,
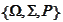where
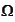is the total event space,
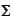is a collection of subsets of
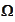equipped with set operations and
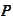is a set function acting
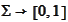with the
properties
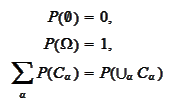for any at most countable collection of sets
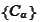such
that
.
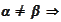
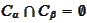Conditional probability
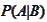of
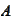conditionally on
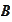is defined as
|
|
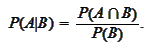
(Bayes formula)
|
If the whole space
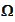is represented as some disjoint union
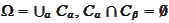then for any
|
|
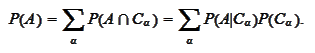
(Total probability rule)
|
The last relationship is called "the total probability rule".
Conditional probability has transitive property:
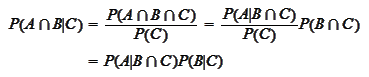hence,
|
|
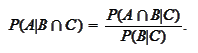
(Transitive bayes formula)
|
Suppose we are facing calculation of the quantity
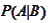and the quantity
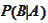is easily computable. The repeated application of the Bayes formula expresses
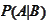in terms of
.
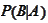Indeed, the Bayes formula is symmetrical:
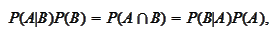hence
The properties
(
Total_probability_rule
),(
Transitive_Bayes_formula
)
and (
Inversion_remark
) are used repeatedly in
the following chapters.
|
