e consider choosing optimal
trading strategy under the real world probability measure. The optimality is
defined in terms of maximization of utility function of final
wealth:
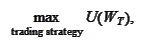 where the
where the
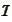 is the time horizon,
is the time horizon,
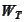 is the final wealth and
is the final wealth and
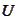 is
a concave function.
is
a concave function.
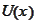 is slightly increasing for large
is slightly increasing for large
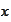 because we would like to make money but not too much because of risk aversion.
Also,
because we would like to make money but not too much because of risk aversion.
Also,
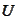 is
sharply decreasing for negative
is
sharply decreasing for negative
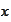 because we do not like to loose money. We are going to show that such setup
leads to delta hedging if the market is complete.
because we do not like to loose money. We are going to show that such setup
leads to delta hedging if the market is complete.
The reference for this section is
[Yang]
.
Notation
We introduce the following notations:
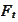 is the equilibrium (optimal trading strategy, expected utility maximizing)
price of an option,
is the equilibrium (optimal trading strategy, expected utility maximizing)
price of an option,
Definition
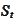 is the stock price,
is the stock price,
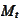 is the amount on the margin account.
is the amount on the margin account.
The sum
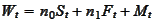 is the "wealth".
is the "wealth".
The pair
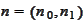 is trading strategy.
is trading strategy.
We introduce the lower case notation for all processes as follows:
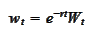 for any
for any
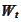 .
.
Claim
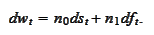
Claim
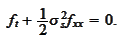
We obtained the Black-Scholes equation.
|