Proof
Let
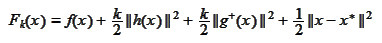 for
for
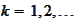
Consider the
problems
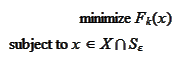
|
|
(Penalized problem)
|
where
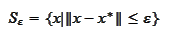 and
and
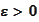 is such that
is such that
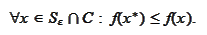
By the classic version of the Weierstrass theorem there exists a solution
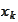 of the problem (
Penalized problem
) for every
of the problem (
Penalized problem
) for every
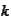 .
In
particular,
.
In
particular,
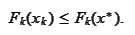 Note that
Note that
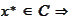
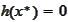 and
and
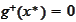 .
Hence, we rewrite the last inequality
as
.
Hence, we rewrite the last inequality
as
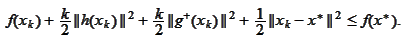
|
|
(FJ proof 1)
|
By construction,
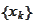 is a bounded sequence. Therefore, is has one or more limit points
is a bounded sequence. Therefore, is has one or more limit points
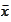 .
.
The
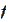 is smooth, hence,
is smooth, hence,
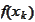 is bounded.
Therefore,
is bounded.
Therefore,
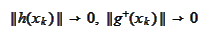 because otherwise
because otherwise
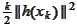 and
and
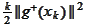 cannot be bounded by the
cannot be bounded by the
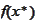 .
.
Thus, all the limit points
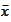 are feasible:
are feasible:
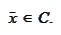 Therefore, by the construction of
Therefore, by the construction of
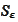 and
and
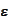 ,
,
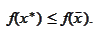
|
|
(FJ proof 2)
|
By passing to the limit the inequality (
FJ proof 1
)
and combining with (
FJ proof 2
)we
conclude
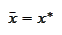 for every limit point
for every limit point
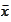 .
Thus
.
Thus
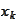 is convergent and
is convergent and
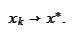
According to the proposition (
Minimum
of a smooth
function
)
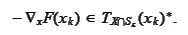 By convergence
By convergence
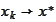 ,
for large enough
,
for large enough
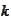 the
the
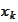 is inside
is inside
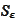 ,
hence
,
hence
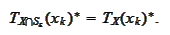 We restrict our attention to such
We restrict our attention to such
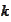 .
.
We
calculate
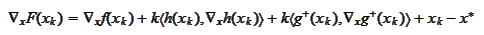
|
|
(FJ proof 3)
|
and introduce the
notation
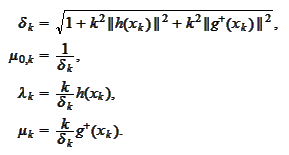 Note that the sequence of
Note that the sequence of
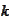
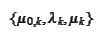 is
bounded:
is
bounded:
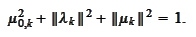 Hence, it has a limit point
Hence, it has a limit point
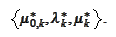
By dividing (
FJ proof 3
) with
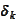 we obtain
we obtain
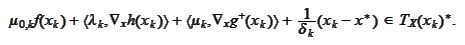 We pass the last relationship to the limit
We pass the last relationship to the limit
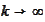 and arrive
to
and arrive
to
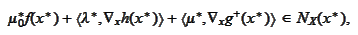
(compare with the definition (
Normal cone
)).
To see that the statement (4) holds, note that by construction of
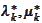 ,
,
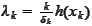 ,
if
,
if
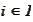 then
then
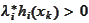 for large enough
for large enough
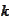 .
If
.
If
 then the
then the
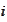 -th
component of
-th
component of
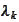 :
:
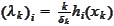 has to vanish as
has to vanish as
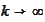 .
Hence, if
.
Hence, if
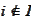 then
then
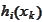 vanishes quicker than any of the
vanishes quicker than any of the
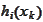 for
for
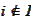 .
The consideration for
.
The consideration for
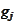 is identical.
is identical.