et
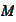 be a subset of
be a subset of
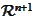 .
The
.
The
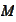 may have common points with the
may have common points with the
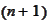 -th
coordinate axis. We introduce the
quantity
-th
coordinate axis. We introduce the
quantity
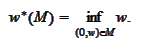
A normal vector to a nonvertical hyperplane may be normalized to a form
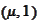 .
A nonvertical hyperplane that crosses the
.
A nonvertical hyperplane that crosses the
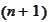 -th
coordinate axis at the point
-th
coordinate axis at the point
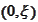 and has a normal vector
and has a normal vector
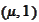 has the
representation
has the
representation
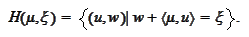 Indeed,
Indeed,
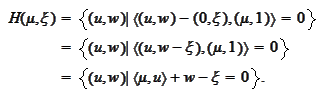
The set
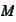 is contained in the upper half plane of
is contained in the upper half plane of
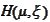 iff
iff
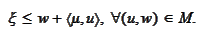 Hence, the
quantity
Hence, the
quantity
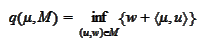 is the maximum
is the maximum
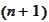 -th
axis crossing level for all hyperplanes that contain the set
-th
axis crossing level for all hyperplanes that contain the set
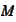 in the upper half space and have the normal vector
in the upper half space and have the normal vector
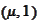 .
.
The
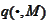 is a concave function.
is a concave function.
We introduce the
quantity
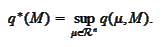
Proof
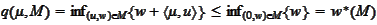 .
.
We investigate the conditions for the equality
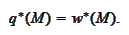 Observe that by definition of these quantities all that is needed is existence
of a supporting hyperplane at a point
Observe that by definition of these quantities all that is needed is existence
of a supporting hyperplane at a point
 .
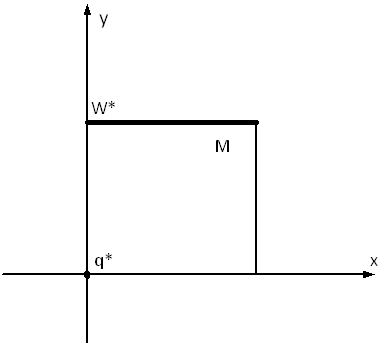
The pictures (
Crossing points figure
1
)-(
Crossing points figure 3
)
show basic examples when this may or may not happen.
.
The pictures (
Crossing points figure
1
)-(
Crossing points figure 3
)
show basic examples when this may or may not happen.
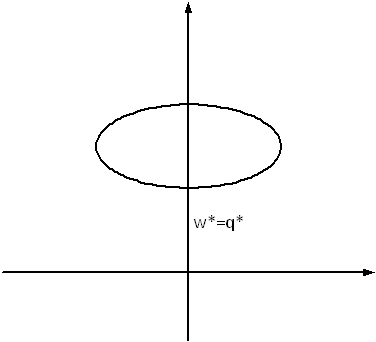
|
Crossing points figure
1
|
|
Crossing points figure 2. The
upper boundary is included in the set. The other boundaries are
excluded.
|
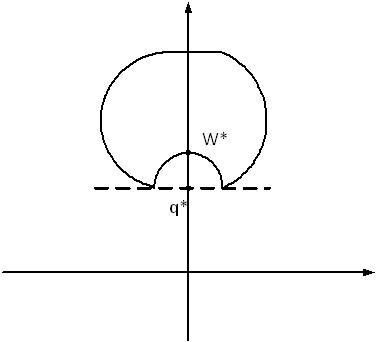
|
Crossing points figure
3
|
|
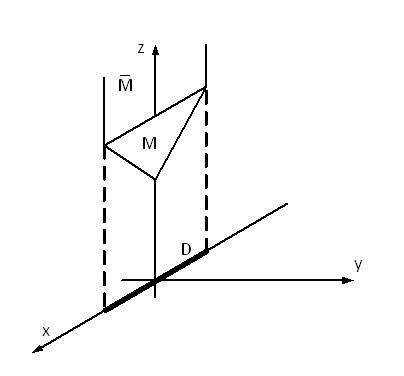
Crossing theorem 2
figure
|
|