roposition
(Directions of recession). Let
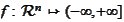 be a closed proper convex function.
be a closed proper convex function.
1. All nonempty level sets
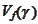 have the same recession cone given
by
have the same recession cone given
by
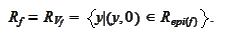
2. If one nonempty level set is compact then all the level sets are compact.
If
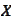 and
and
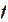 has no common direction of recession then the minimum cannot escape to
infinity. Such intuition may be formalized into a proof by considering
intersections of the nested compact convex sets
has no common direction of recession then the minimum cannot escape to
infinity. Such intuition may be formalized into a proof by considering
intersections of the nested compact convex sets
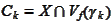 with the sequence
with the sequence
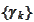 converging to the
converging to the
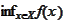 .
The following proposition is a consequence of the same observation and the
propositions (
Principal intersection
result
),(
Linear intersection
result
) and (
Quadratic
intersection result
).
.
The following proposition is a consequence of the same observation and the
propositions (
Principal intersection
result
),(
Linear intersection
result
) and (
Quadratic
intersection result
).
|