et
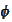 be a function
be a function
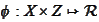 where the
where the
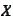 and
and
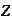 are subsets of
are subsets of
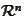 and
and
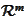 respectively. We always
have
respectively. We always
have
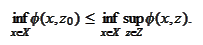 Therefore,
Therefore,
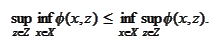 In this section we investigate the conditions for
In this section we investigate the conditions for
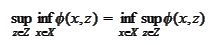
|
|
(Minimax equality)
|
and attainment of the sup and inf.
Proposition
(Saddle point's defining property).
The pair
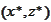 is a saddle point iff the relationship (
Minimax
equality
) holds and
is a saddle point iff the relationship (
Minimax
equality
) holds and
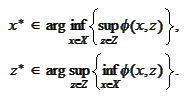
We introduce the function
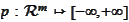 given
by
given
by
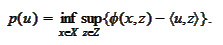
|
|
(definition of minmax p)
|
We will be using results of the section
(
Min common and max
crossing point section
). Following that section we define
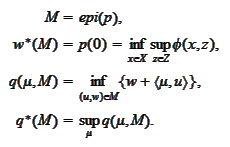
|