roposition
For any convex function
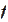
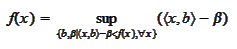
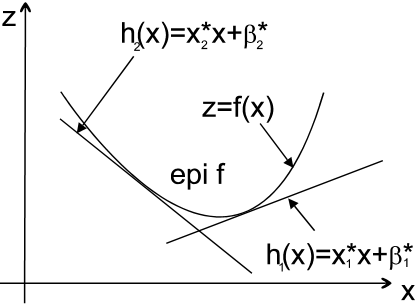
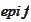 is the intersection of the upper half planes.
is the intersection of the upper half planes.
|
Corollary
The set
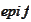 is equal to intersection of the upper half-planes defined by the hyperplanes
from proof of the previous statement.
is equal to intersection of the upper half-planes defined by the hyperplanes
from proof of the previous statement.
Let us denote
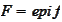 .
Let us introduce a
set
.
Let us introduce a
set
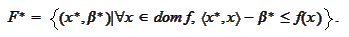 Such set is not empty and it is an epigraph of some function because if
Such set is not empty and it is an epigraph of some function because if
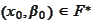 then
then
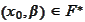 for all
for all
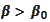 .
Let us denote such function
.
Let us denote such function
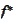 .
By
definition
.
By
definition
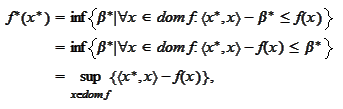
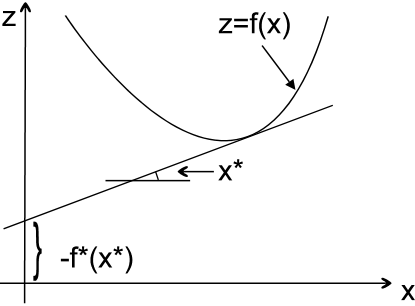
Geometrical meaning of
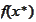 .
.
|
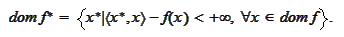
Let us introduce
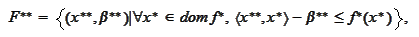
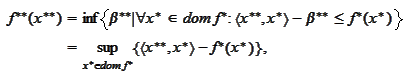
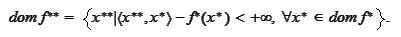 Observe that
Observe that
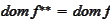 .
Indeed,
.
Indeed,
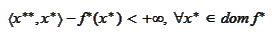 means that
means that
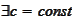
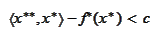 or
or
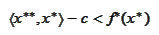 where the
where the
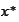 and
and
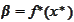 run through all the hyperplanes that define
run through all the hyperplanes that define
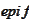 .
For the same reason the infimum of such
.
For the same reason the infimum of such
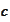 is the
is the
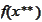 :
:
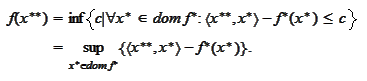
The closure part:
 comes from the fact that taking affine envelopes includes boundary points of
the
comes from the fact that taking affine envelopes includes boundary points of
the
 into the final result
into the final result
 .
.
|