ntersection of nested closed compact sets is not empty.
Intersection of nested unbounded closed convex sets may be empty. Consider
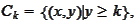
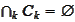 .
The sets
.
The sets
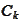 escape to infinity along the common direction of recession
escape to infinity along the common direction of recession
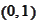 .
However, if all directions of recession are included in a common linearity
space then this cannot happen as stated in the proposition below.
.
However, if all directions of recession are included in a common linearity
space then this cannot happen as stated in the proposition below.
To see that the
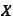 has to be linear consider
has to be linear consider
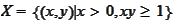 and
and
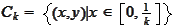 .
Such
.
Such
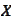 and
and
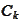 fail only the linearity requirement and the conclusion of the theorem.
fail only the linearity requirement and the conclusion of the theorem.
|