A hyperplane
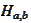 may be represented as
may be represented as
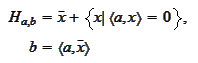 for any fixed
for any fixed
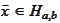 .
.
Proposition
(Separating hyperplane theorem). If
the
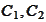 are two nonempty disjoint convex sets then there is a hyperplane that
separates them.
are two nonempty disjoint convex sets then there is a hyperplane that
separates them.
Two nonempty convex disjoint sets
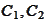 are not necessarily strictly separated. For example,
are not necessarily strictly separated. For example,
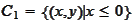 ,
,
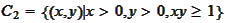 do not have a strictly separating hyperplane.
do not have a strictly separating hyperplane.
Let
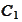 and
and
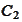 be two disjoint closed convex subsets of
be two disjoint closed convex subsets of
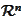 .
To investigate the conditions for
.
To investigate the conditions for
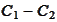 to be closed we introduce the subset
to be closed we introduce the subset
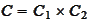 of
of
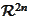 ,
note that the transformation
,
note that the transformation
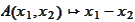 is linear and seek to apply the proposition
(
Preservation of closeness
result
). We note that
is linear and seek to apply the proposition
(
Preservation of closeness
result
). We note that
 is closed and
convex,
is closed and
convex,
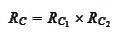 and
and
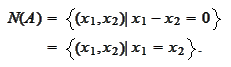 The condition
The condition
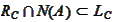 of the proposition (
Preservation
of closeness result
)
becomes
of the proposition (
Preservation
of closeness result
)
becomes
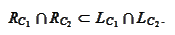
We arrive to the following additional sufficient conditions for strict
separation.
Proposition
(Intersection of half-spaces). The
closure of convex hull of a set
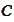 is the intersection of all closed half-spaces that contain
is the intersection of all closed half-spaces that contain
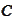 .
.
Proof
If there is a point in
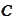 that is not contained in the intersection of half-planes then we arrive to
contradiction by using the theorem
(
Supporting hyperplane theorem
).
that is not contained in the intersection of half-planes then we arrive to
contradiction by using the theorem
(
Supporting hyperplane theorem
).
Let
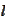 be a line
be a line
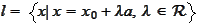 for some
for some
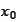 .
The definition of the proper separation requires that
.
The definition of the proper separation requires that
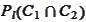 is a single point or nothing and
is a single point or nothing and
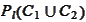 consists of more then one point.
consists of more then one point.
The sets
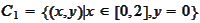 and
and
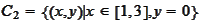 may not be properly separated.
may not be properly separated.
The sets
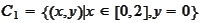 and
and
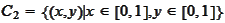 are properly separated by the x-axis
are properly separated by the x-axis
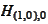 .
.
|