Notation
We imply
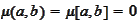 if
if
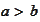 .
.
Proposition
(Vague precompactness of s.p.m.) For
any sequence
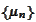 of s.p.m. there is a subsequence
of s.p.m. there is a subsequence
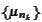 that converges vaguely to a s.p.m.
that converges vaguely to a s.p.m.
Proof
A function
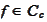 may be
may be
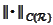 -approximated
by a sequence of piecewise constant function. For the piecewise functions the
statement is apparent. This argument works in both directions.
-approximated
by a sequence of piecewise constant function. For the piecewise functions the
statement is apparent. This argument works in both directions.
Definition
(Tight sequence). The sequence of measures
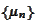 is called "tight"
if
is called "tight"
if
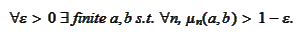
Proposition
(Precompactness of a
tight sequence of p.m.). Let
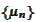 be a tight sequence of p.m. The there is a subsequence that converges vaguely
to a p.m..
be a tight sequence of p.m. The there is a subsequence that converges vaguely
to a p.m..
|