e proceed to verify that the
expression
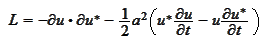is a Lagrangian for the heat
equation
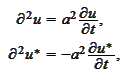
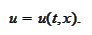
We form the "action" function as
follows
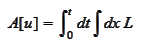and calculate the
variation
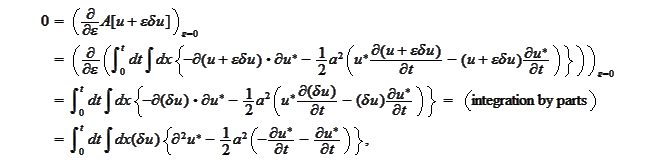hence,
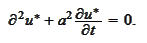Similarly, the calculation of
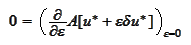leads
to
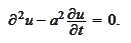
Unfortunately, general Hamiltonian technique is not applicable to the heat
equation because the defining equation for p
(
generalized impulse equation
)
does not have a solution for q
(
generalized impulse solution
).
|
