he duality between SDE and PDE allows to find change-of-variable
transformations that reduce complexity of the problem.
Consider two
SDEs
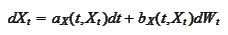and
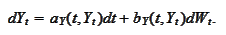We are interested in evaluation of the expectation
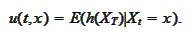We already established in section
(
Backward_equation_section
) that the
function
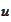is a solution of the following PDE
problem:
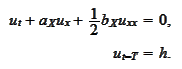Assume existence of a one-to-one
relationship
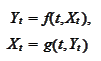for some functions
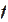and
.
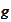We
calculate
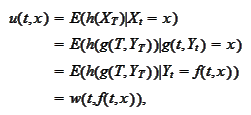where the function
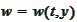is a solution of the PDE
problem
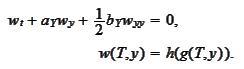
We provide two examples.
|
