e study properties of a process
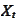 given by the
SDE
given by the
SDE
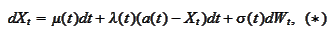 where
where
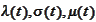 and
and
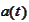 are some regular deterministic functions and
are some regular deterministic functions and
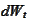 is a standard Brownian motion. We introduce a process
is a standard Brownian motion. We introduce a process
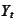 :
:
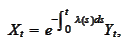 then
then
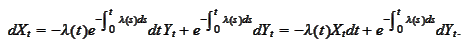 We substitute (*) and
obtain
We substitute (*) and
obtain
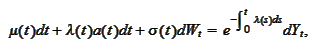 or
or
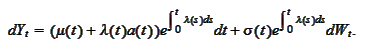 We integrate the last relationship for
We integrate the last relationship for
![$t\in\lbrack0,T]$](graphics/notesCF__0__2905.gif) and
obtain
and
obtain
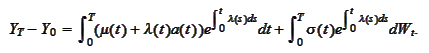 After multiplication by
After multiplication by
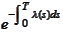 we conclude
we conclude
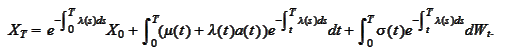
To explain relevance of the mean reverting equation let us consider an
equation
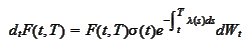 frequently used as a first-approximation simplistic model for a forward curve
frequently used as a first-approximation simplistic model for a forward curve
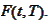 The
The
 is the observation time and the
is the observation time and the
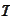 is the expiration time. The front end of the curve is most volatile. The
volatility decreases as
is the expiration time. The front end of the curve is most volatile. The
volatility decreases as
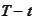 increases. This is a simple but realistic model of propagation of new
information through forward curve.
increases. This is a simple but realistic model of propagation of new
information through forward curve.
We integrate the above equation as
follows:
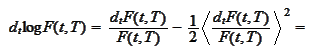
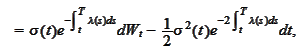
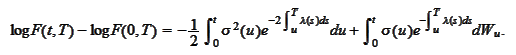 We introduce the "spot" price
We introduce the "spot" price
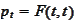 and compute the SDE for the process
and compute the SDE for the process
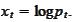 We
have
We
have
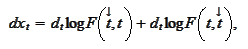 where the arrow marks application of the
where the arrow marks application of the
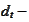 operation.
operation.
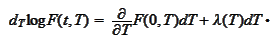
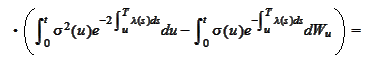
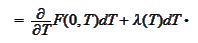
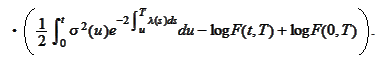 Hence,
Hence,
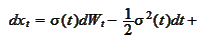
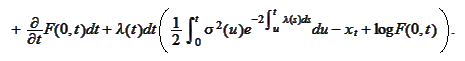 We conclude that the SDE for the
We conclude that the SDE for the
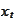 is mean reverting with the parameters
is mean reverting with the parameters
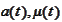 given
by
given
by
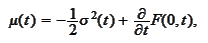
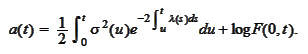
Note that
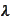 is the mean-reversion parameter and the slope of the forward volatility curve.
is the mean-reversion parameter and the slope of the forward volatility curve.
|