et
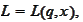
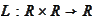be a smooth function. We introduce the
action
functional
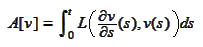taking vector functions of
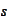and producing a number. We consider a problem of minimization of
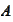across a variety of smooth functions
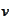with fixed values of
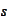at
the ends of the interval
![$\left[ 0,t\right] $](graphics/notesCF__0__3730.gif)
.
If a function
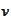minimizes
![$A\left[ v\right] $](graphics/notesCF__0__3732.gif)
then we must have for any perturbation function
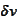and number
:
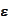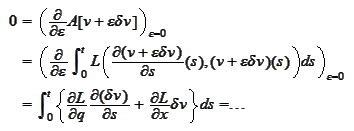We integrate the first term by parts and use the fact that the perturbation
must be zero at the ends of the
interval:
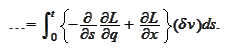The above is true for any
.
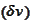Hence
|
|
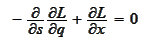
(Euler Lagrange equation)
|
when evaluated at the minimizing function
.
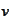The last equation is called the Euler-Lagrange equation.
|
