e would like to extend a solution
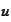of the equation (
First order PDE
) from a
surface of boundary condition along some family of
curves
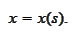We seek an effective way to define such a family. We hope to reduce the non
linear PDE (
First order PDE
) to a system of
ODEs.
Notation
We introduce the
notations
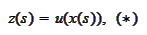
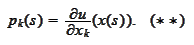
We differentiate the definition (*) along the parameter
:
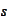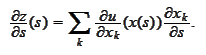We also differentiate the (
First order PDE
)
along
for every
:
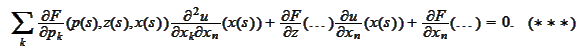We would like to get rid of the derivative
,
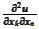hence, we differentiate the definition (**) of
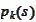with respect to
:
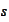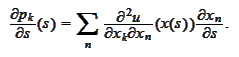Therefore, if we would
require
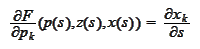we would easily remove the
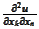from
(***):
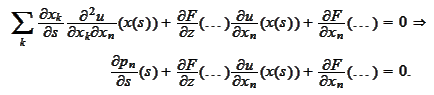We collect our results as follows.
Definition
The functions
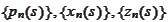that satisfy the system of
ODE
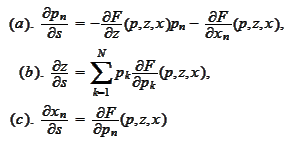are called characteristics of the PDE (
First order
PDE
).
If a function
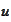solves the PDE and
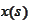solves (c) with
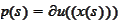and
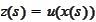then p and z solve (a) and (b). One may always attempt to go in reverse:
extend a solution of PDE from some (consistent) boundary condition using a
family of solutions of (a),(b),(c).
|
