e would like to calculate the
expression
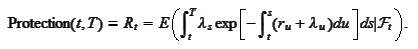We proceed similarly to the previous section. We calculate the
drift
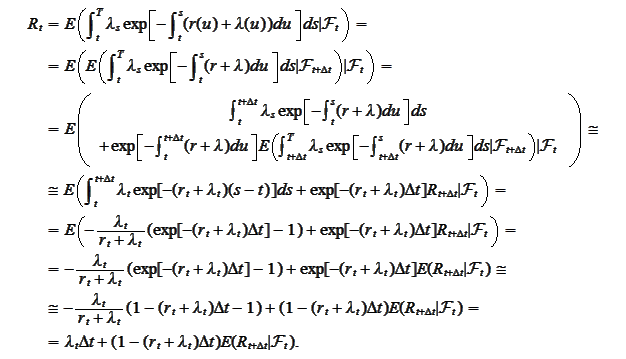Hence,
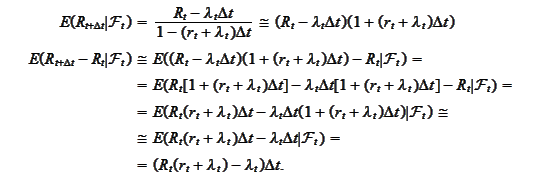We conclude
that
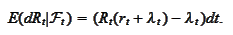Following logic of the previous section we will be seeking for a function
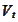of the
form
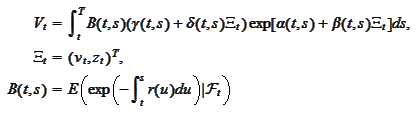for some deterministic functions
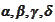having the
property
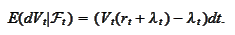We
have
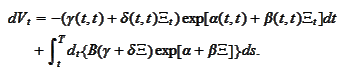We introduce
notation
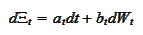with
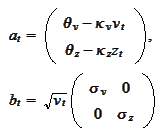then
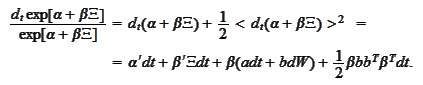Hence we calculate the drift part
as
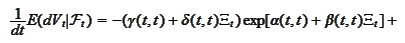
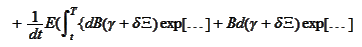
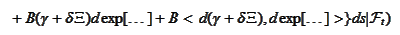
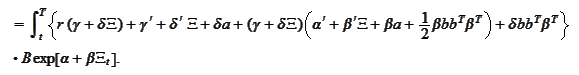We want the above expression to be
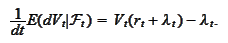Hence, it suffices to
have
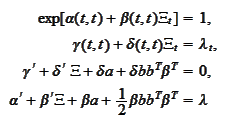where we made an assertion that
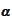and
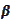are the same as in the previous section and
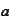and
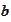are given by the same
expressions
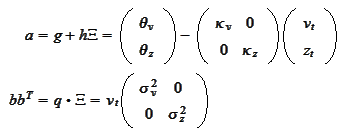Consequently,
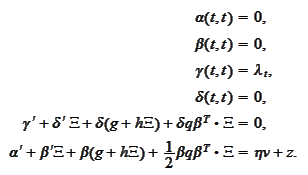We separate the
coordinates
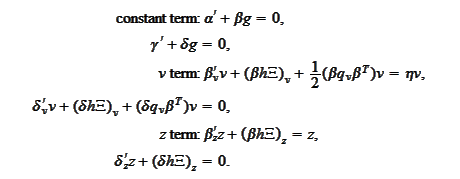We substitute the expressions for the
.
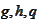The equations for
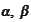have been calculated before. The equations for
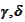resolve
to
|
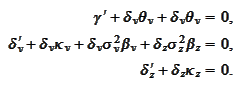
