e would like to calculate the
expression
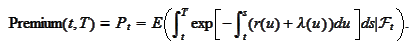Observe that
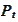is not a martingale.
Indeed,
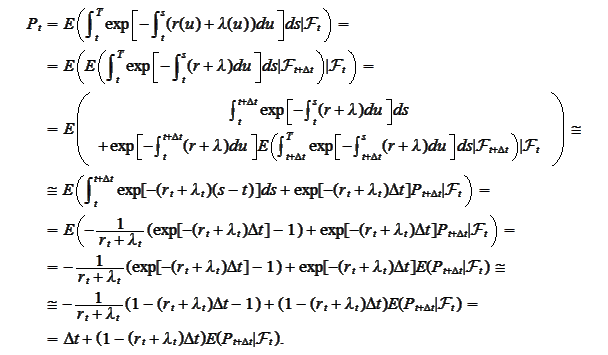Hence,
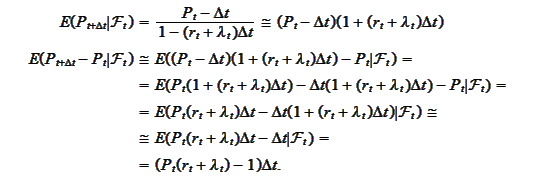We conclude
that
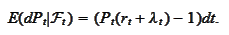Therefore,
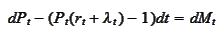for some martingale
.
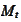We want to replicate the
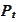with some function of state variables
.
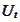If successful, such function should
satisfy
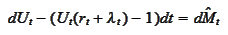for some martingale
.
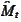If both martingales also coincide at final time
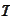then we will have the
equality:
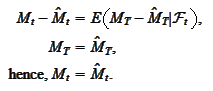
We will seek for
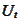in the
form
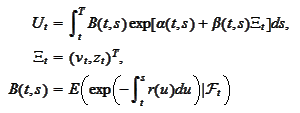where the
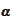and
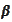are some deterministic functions.
Hence,
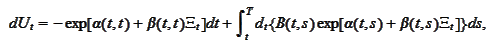We introduce
notation
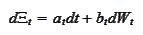with
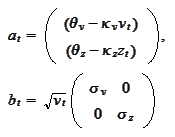then
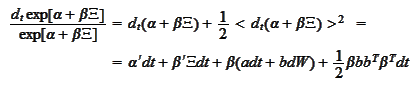hence we calculate the drift part as
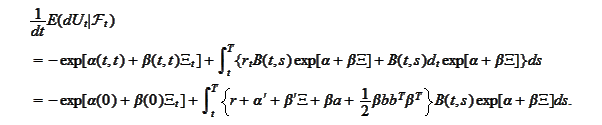We want the above expression to be
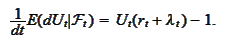Hence, it suffices to
have
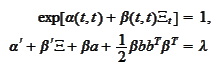where
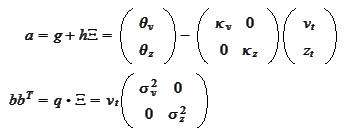Consequently,
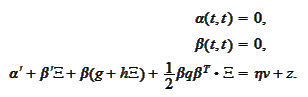We separate the
coordinates
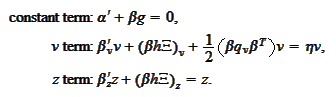We substitute the expressions for the
.
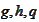The equations resolve
to
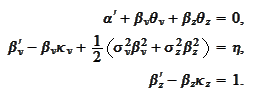These coincide with the equations (17) in the article because (in article
[CarrWu2006a]
's
notation)
|
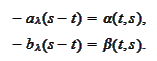
