e summarize the situation as follows. We have a 3-dimentional process
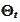 given by the
equation
given by the
equation
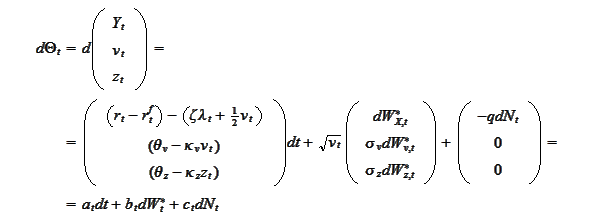 where we use the
notation
where we use the
notation

We calculate the
increment
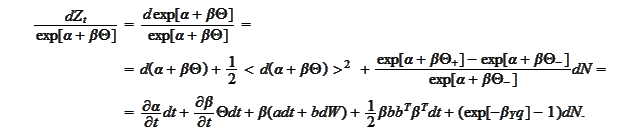 For
For
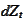 to be a martingale, we must
have
to be a martingale, we must
have
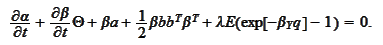 We introduce the notations
We introduce the notations
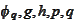 as
follows:
as
follows:
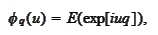
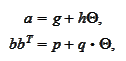
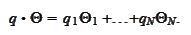 Consequently, we
have
Consequently, we
have
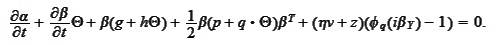 We separate terms with every power and coordinate of
We separate terms with every power and coordinate of
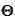 :
:
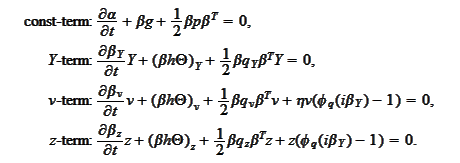
We now recover the expressions for
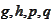 before we substitute it into the above ODEs for
before we substitute it into the above ODEs for
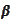 and
and
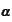 .
By comparing
definitions
.
By comparing
definitions
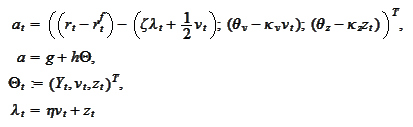 we
see
we
see
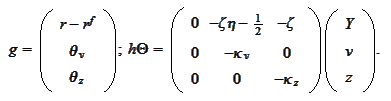 Similarly for
Similarly for
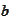 we have
definitions
we have
definitions
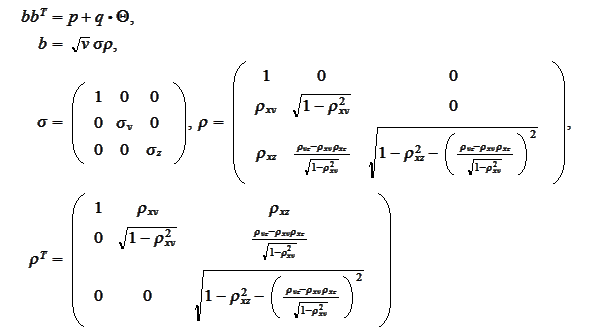 hence
hence
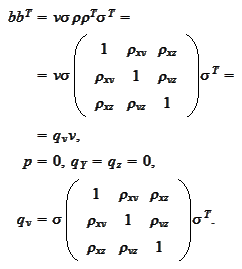 Also,
Also,
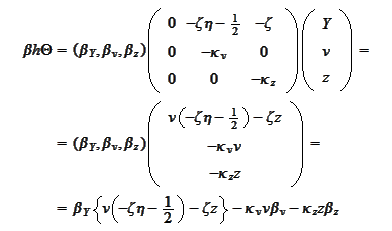
We now recover the ODEs for
 :
:
We calculate the expression
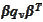 under assumption that
under assumption that
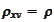 is the only non-zero
correlation:
is the only non-zero
correlation:
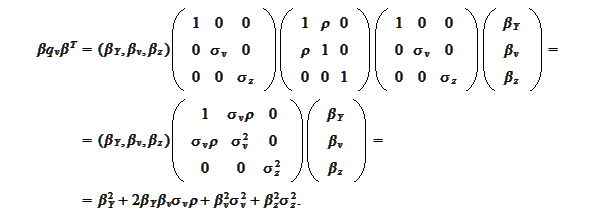
Hence,
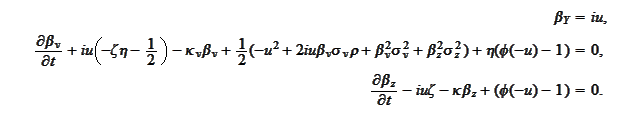 Equivalently,
Equivalently,
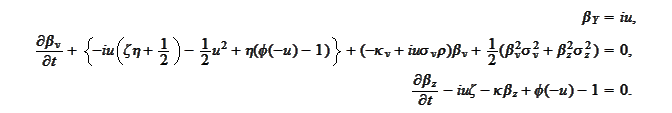
The equation for
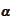 resolves
to
resolves
to
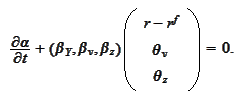
We summarize the results up to this point as
follows
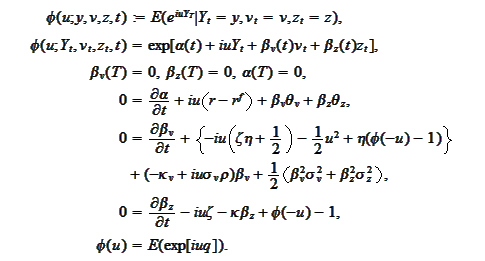
We would like to compare these results with the results of the paper
[CarrWu2006a]
. Hence, we perform additional
transformations.
We calculated earlier
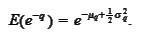 Hence,
Hence,
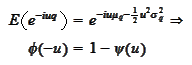 where the
where the
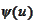 is the notation of the paper. We change variable from
is the notation of the paper. We change variable from
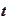 to
to
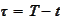 ,
hence,
,
hence,
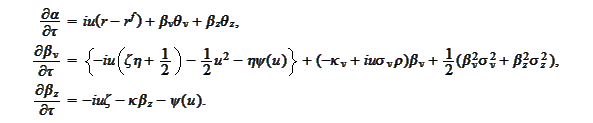 The last expressions compare exactly with the paper
[CarrWu2006a]
.
The last expressions compare exactly with the paper
[CarrWu2006a]
.
|