ollowing the common business practice we will assume in this section that the
future distribution of a traded instrument
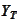is tracked via a volatility smile. We will utilize the notation of the formula
(
Black Scholes formula
) for the
undiscounted call
price:
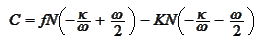where
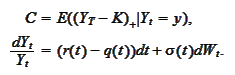We use the
notation
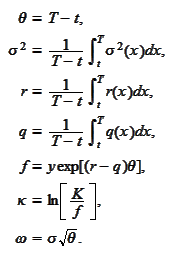Assume that
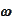has dependence on
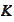derived from dependence of
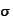on
.
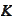This is the "volatility smile" practice. The Black-Scholes formula is fitted
into marked quotes by introducing dependence of the parameter
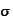on
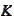and
.
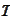We are going to calculate the implied distribution of the random variable
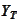via double differentiation of
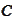and use the formula (
Fair Variance
vs Log contract
).
We proceed with calculation of the
derivative:
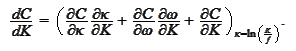By the formula (
Black Scholes property
1
)
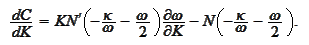Also,
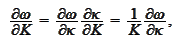hence,
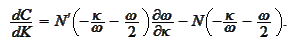Consequently,
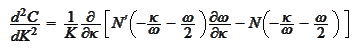where
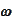is a
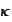dependent function. We use the notation
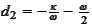introduced in (
Black Scholes
formula
).
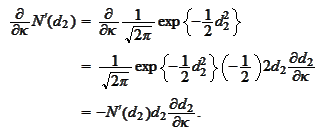Hence,
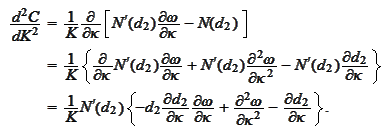
We now invoke the formulas (
Fair
Variance vs Log contract
) and
(
Distribution density via
Call
):
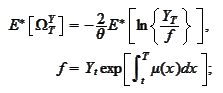
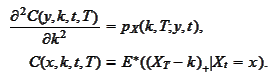Therefore,
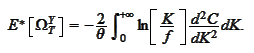We perform the change of
variables
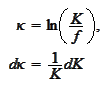and
continue
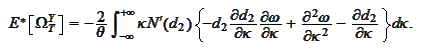The function
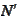is rapidly decaying at infinity. We use such property to perform the following
integration by
parts
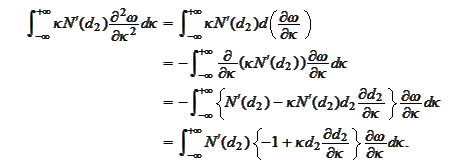We use this result to remove the
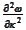term in the expression for
:
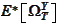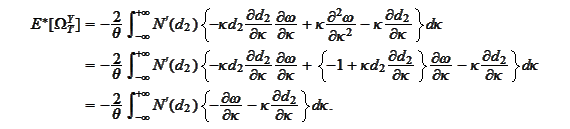We perform the similar integration by
parts:
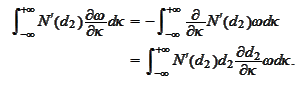and use it to remove the
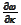term in the expression for
:
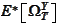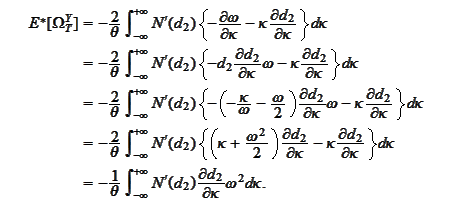Note that since
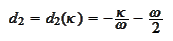then
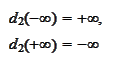hence
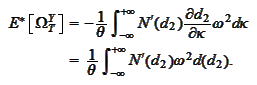
Recall
that
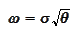where the
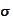is the Black-Scholes volatility. Hence we arrive to the following summary.
|
