uppose a stock
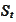 follows the
SDE
follows the
SDE
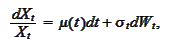
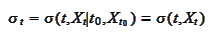 in the risk neutral world. The
in the risk neutral world. The
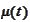 is a deterministic function of time. The
is a deterministic function of time. The
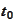 is the moment of observation. We aim to express the volatility
is the moment of observation. We aim to express the volatility
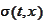 as a function of
as a function of
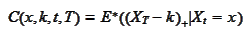 and its derivatives with respect to strike.
and its derivatives with respect to strike.
We use the
representation
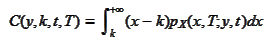 in terms of distribution density
in terms of distribution density
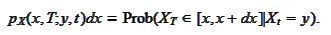 We calculate the
We calculate the
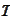 -derivative
-derivative
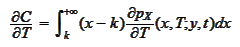 and substitute the equation
(
Forward_Kolmogorov
):
and substitute the equation
(
Forward_Kolmogorov
):
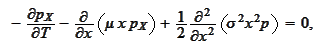
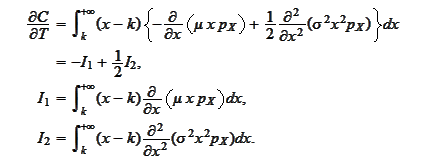
We evaluate each integral via integration by parts and with help of results
(
Distribution density via Call
).
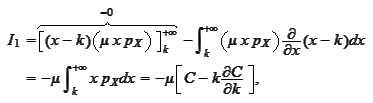
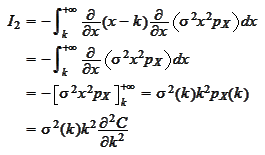
Summary
(Differentiating
call with respect to maturity
1)Assume
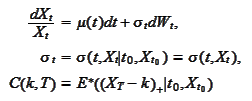 then
then
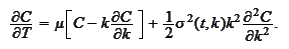
We now switch to a process of the
form
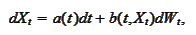
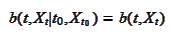 where the function
where the function
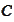 is still given by
is still given by
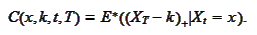 Thus we cannot simply do a
Thus we cannot simply do a
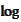 -change
of variables to reduce to the previous case. We repeat our
calculations.
-change
of variables to reduce to the previous case. We repeat our
calculations.
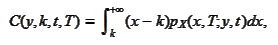
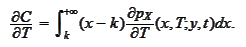 The equation (
Forward_Kolmogorov
) now has
the
form
The equation (
Forward_Kolmogorov
) now has
the
form
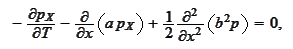
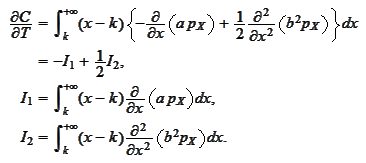 We integrate by parts and use the formulas
(
Distribution density via
Call
):
We integrate by parts and use the formulas
(
Distribution density via
Call
):
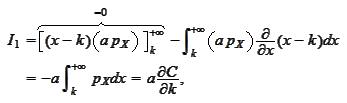
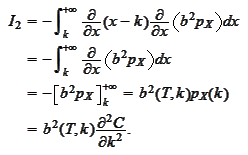
Summary
(Differentiating
call with respect to maturity 2)
Assume
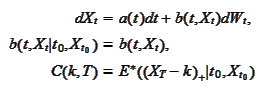 then
then
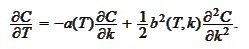
|