The process
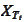 does not need to be Markovian.
does not need to be Markovian.
We proceed to investigate conditions for
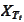 to be Markovian.
to be Markovian.
Let
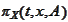 be the transition function for the process
be the transition function for the process
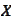 and
and
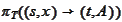 be the transition function for the process
be the transition function for the process
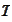 .
We calculate the transition function for the subordinated process
.
We calculate the transition function for the subordinated process
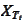 .
For
.
For
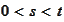 we define a uniform mesh over
we define a uniform mesh over
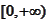 with step
with step
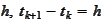 and apply the formula
(
Total_probability_rule
):
and apply the formula
(
Total_probability_rule
):
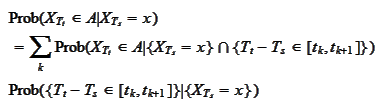 By independence of
By independence of
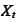 and
and
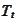 we
simplify
we
simplify
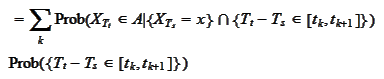 We need the expression
Prob
We need the expression
Prob
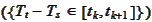 to be well defined for any
to be well defined for any
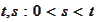 and any however fine mesh
and any however fine mesh
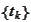 .
This means that the law of
.
This means that the law of
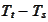 needs to be independent of
needs to be independent of
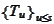 .
Thus
.
Thus
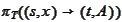 needs to be a function of the form
needs to be a function of the form
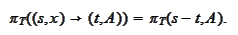 We
continue
We
continue
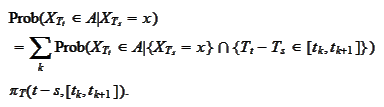 Next, we would like to
write
Next, we would like to
write
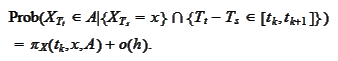 This imposes regularity requirements
This imposes regularity requirements
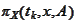 along
along
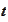 -parameter.
We pass to the limit
-parameter.
We pass to the limit
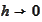 :
:
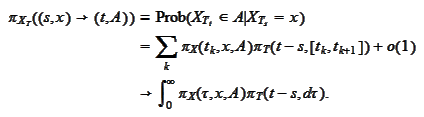 For
For
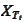 to be Markovian it needs to satisfy the formula
(
Kolmogorov-Chapman equation
),
to be Markovian it needs to satisfy the formula
(
Kolmogorov-Chapman equation
),
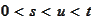 :
:
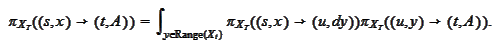 We calculate the
integral
We calculate the
integral
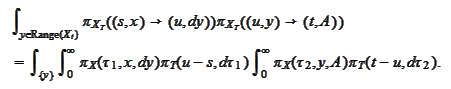 Note that by assumption,
Note that by assumption,
 is Markovian and has the formula
(
Kolmogorov-Chapman
equation
):
is Markovian and has the formula
(
Kolmogorov-Chapman
equation
):
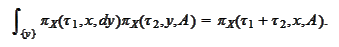 Hence, we
continue
Hence, we
continue
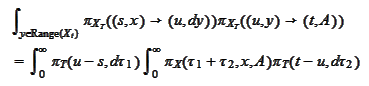 We make a change of variables
We make a change of variables
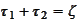
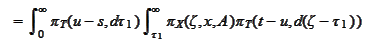 and change the order of
integration
and change the order of
integration
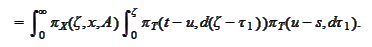 For
For
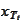 to be Markovian the last expression should be equal to
to be Markovian the last expression should be equal to
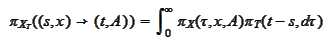 thus we
need
thus we
need
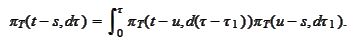 The convolution on the right is a formula for distribution of a sum of two
independent r.v. We conclude that the increments of
The convolution on the right is a formula for distribution of a sum of two
independent r.v. We conclude that the increments of
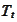 should be infinitely divisible and stationary. We summarize these findings in
the following proposition.
should be infinitely divisible and stationary. We summarize these findings in
the following proposition.
|