e intend to
apply Newton technique to the equation
(
Implicit equation with
penalty term
):
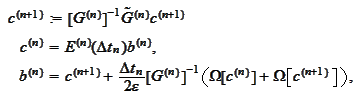 The equation has the
form
The equation has the
form
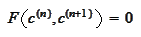 with
with
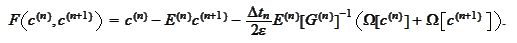 We introduce the convenience
notations
We introduce the convenience
notations
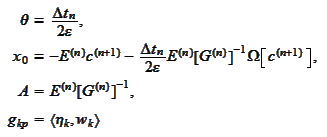 and drop the upperscript
and drop the upperscript
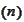 :
:
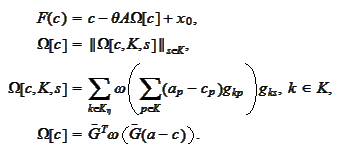
We calculate the matrix of first
derivatives:
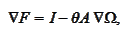
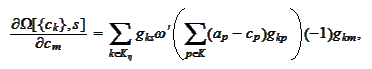
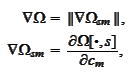
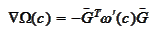 where
where
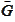 is a Gram
matrix
is a Gram
matrix
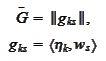
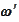 is a diagonal matrix with small
values
is a diagonal matrix with small
values
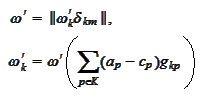 and the matrix
and the matrix
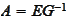 has spectral radius close to 1 (from above).
has spectral radius close to 1 (from above).
The Newton procedure is the
iteration
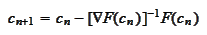 where we
use
where we
use
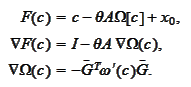 We start Newton iterations
from
We start Newton iterations
from
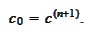 For small time step, the initial position
For small time step, the initial position
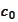 is sufficiently close to the root of
is sufficiently close to the root of
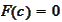 for convergence of Newton iterations.
for convergence of Newton iterations.
Due to smallness of the function
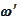 and
boundedness of other components, the matrix
and
boundedness of other components, the matrix
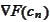 is safely invertible for wide range of parameters.
is safely invertible for wide range of parameters.
Implementation of such approach is implemented in the script soNewton1.py,
located in the directory OTSProjects/python/wavelets2. Experimentation shows
that in order to keep the discrepancy
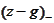 to acceptable size, one has to take
to acceptable size, one has to take
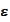 in the area of 1.e-3. If we do not decrease the time step with
in the area of 1.e-3. If we do not decrease the time step with
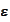 then the Newton procedure diverges. Such extreme stiffness is not a feature of
the problem under consideration but a limitation of the Newton technique. We
propose a more robust procedure in the following section.
then the Newton procedure diverges. Such extreme stiffness is not a feature of
the problem under consideration but a limitation of the Newton technique. We
propose a more robust procedure in the following section.
|