he origin
of mean reverting equation as stated below was discussed in the section
(
Solving
one dimensional mean reverting equation
).
According to the summary (
Free
boundary problem 2
), the function
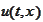 also solves the following free boundary problem.
also solves the following free boundary problem.
Let
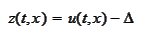 and
and
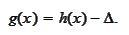
We multiply the above PDE with a smooth function
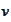 ,
,
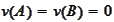 ,
integrate over
,
integrate over
![$\left[ A,B\right] $](graphics/notesCF__2__1572.gif) and do integration by parts. We
get
and do integration by parts. We
get
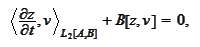
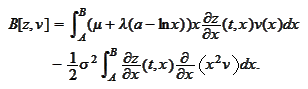 We add the penalty term according to the recipe
(
Variational
inequalities in maximization case
). We arrive to the following penalized
problem.
We add the penalty term according to the recipe
(
Variational
inequalities in maximization case
). We arrive to the following penalized
problem.
|