et us review.
We stop evolution in time face the problem of taking
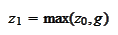 where
where
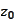 and
and
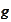 are two known functions. These functions are given by the columns
are two known functions. These functions are given by the columns
 and
and
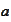 :
:
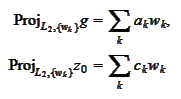 where
where
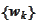 are bases in
are bases in
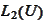 of manageable size and
of manageable size and
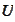 is a rectangular domain in
is a rectangular domain in
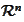 .
We keep the size of
.
We keep the size of
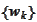 manageable by using sparse tensor product. However, in multiple dimensions
manageable by using sparse tensor product. However, in multiple dimensions
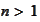 we are prohibited from taking the
sums
we are prohibited from taking the
sums
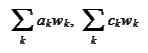 because these would have to be described as piecewise polynomials on straight
product
because these would have to be described as piecewise polynomials on straight
product
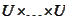 .
Such descriptions would have unmanageable size.
.
Such descriptions would have unmanageable size.
To overcome this difficulty we construct
instead
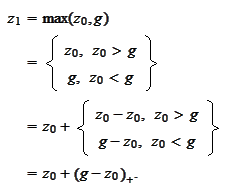
In the previous sections we construct a procedure that adaptively approximates
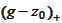 by a linear combination of
by a linear combination of
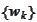 .
We make an observation that for corrected
.
We make an observation that for corrected
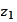 the difference
the difference
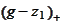 should not have positive component. Then we subtract adaptively non-negative
functions until we reach our goal.
should not have positive component. Then we subtract adaptively non-negative
functions until we reach our goal.
If we use plain pyramid functions in multidimensional situation then we would
have to subtract a lot of them. It would not be efficient. How do we
efficiently select a good function to subtract? We can subtract several
pyramid functions with non-overlapping support in parallel. We also can
subtract probing functions with good approximation properties. For example, we
could use the crudification operator, see the definitions
(
Crudification
operator
),(
Crudification operator
2
). The difficulty with taking
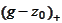 is not the size of the basis but the size the piecewise polynomial
representation. By using the crudification operator, we control the size of
representation. We crudify representations of
is not the size of the basis but the size the piecewise polynomial
representation. By using the crudification operator, we control the size of
representation. We crudify representations of
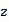 and
and
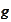 ,
calculate the crudified version of
,
calculate the crudified version of
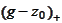 and use it as
and use it as
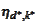 in the procedure of the section
(
Mix
of backward induction and penalty term approaches II
).
in the procedure of the section
(
Mix
of backward induction and penalty term approaches II
).
The crudification of the coordinate columns is performed as follows. Let
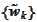 be a relatively small crudified basis. We
introduce
be a relatively small crudified basis. We
introduce
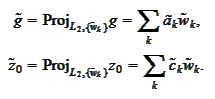 We can efficiently calculate
We can efficiently calculate
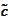 for any
for any
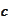 .
Indeed,
.
Indeed,
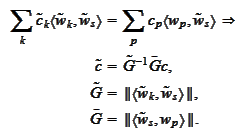 The matrixes
The matrixes
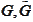 are of the form
are of the form
 see the sections (
Solving
N-dimensional PDEs
) and
(
Reduction
to system of linear algebraic equations for Black PDE
).
see the sections (
Solving
N-dimensional PDEs
) and
(
Reduction
to system of linear algebraic equations for Black PDE
).
|