e continue calculations of the section
(
Unscented transformation
section
) and use the summary (
Unscented
mean summary
).
Similarly to the previous section
(
Unscented mean section
) we write
Taylor expansions for quantities of
interest:
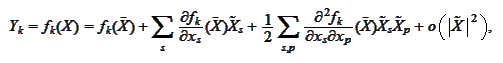
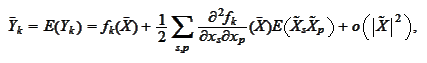
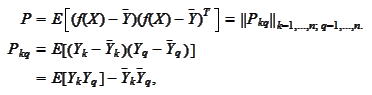
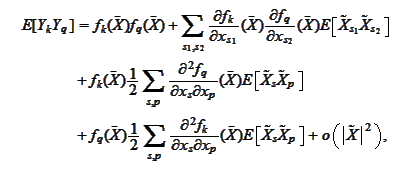
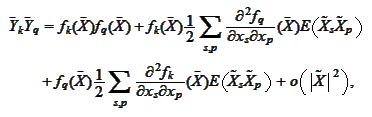
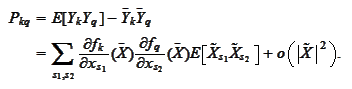The above matrix is approximated with the sum
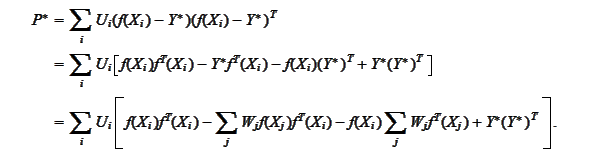We
set
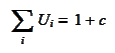for some
,
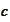then
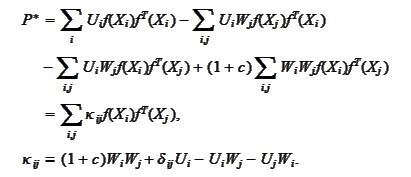We substitute the Taylor expansions for
:
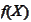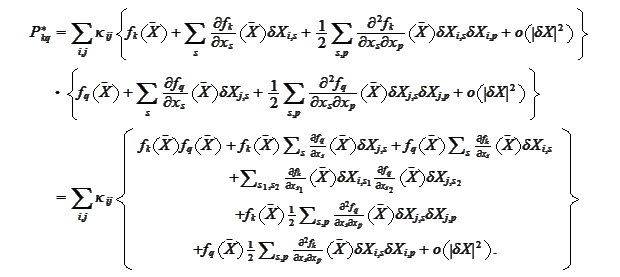By comparing the expressions for
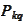and
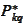we conclude that it is enough to have the following properties of
:
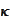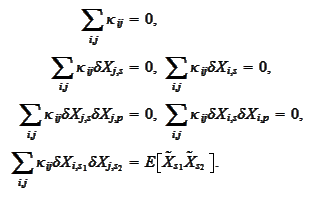The first five would be satisfied
if
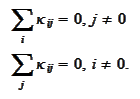The above conditions are true by the structure of
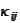and the properties
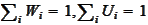and if we set
.
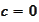Indeed,
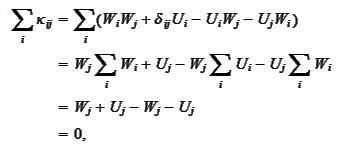
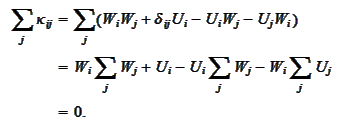We next investigate the
requirement
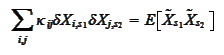where the
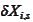where calculate in the previous
section
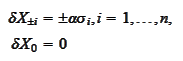and the
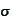comes from the
relationship
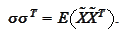Note that
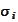is
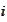-th
column of
,
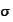hence the
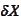satisfy
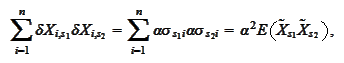hence,
and the
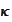is required to have the
property
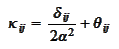where
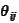is any matrix such
that
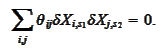It is enough to
set
|
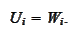
