efore we proceed with derivations for a linear version of the Kalman filter
we perform some general calculation we will use repeatedly. We would like to
evaluate the following
integral
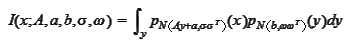 where the
where the
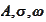 are matrixes and
are matrixes and
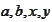 are vectors. We
calculate
are vectors. We
calculate
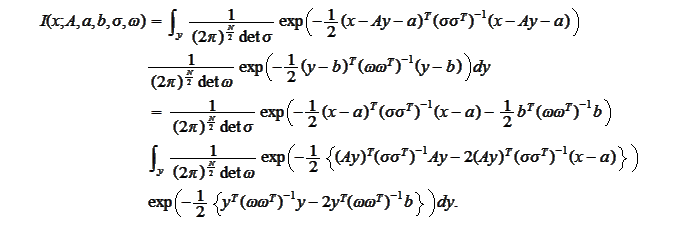 The
The
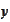 -integral
is evaluated via completion of the
square:
-integral
is evaluated via completion of the
square:
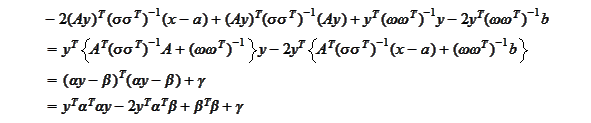 for some
for some
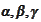 .
Hence, we
require
.
Hence, we
require
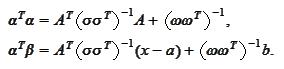 The expression
The expression
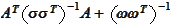 is positive and symmetrical, therefore such
is positive and symmetrical, therefore such
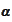 exists. We
continue
exists. We
continue
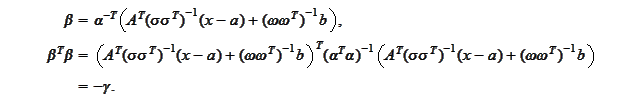 We
have
We
have
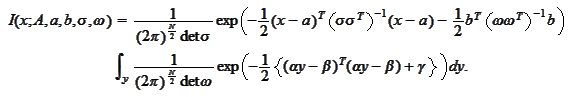 We perform the change
We perform the change
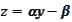 in the integral. The Jacobian is
in the integral. The Jacobian is
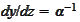 .
The integral is
.
The integral is
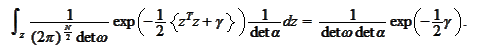 We collect our results
together,
We collect our results
together,
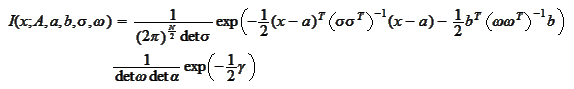
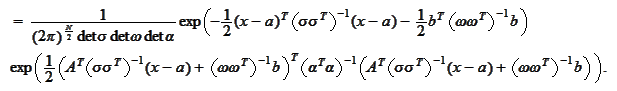 Observe that if
Observe that if
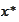 is such
that
is such
that
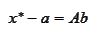 then
then
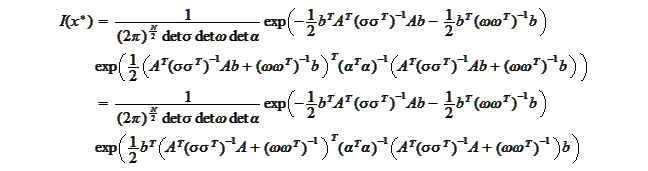 with
with
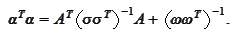 Hence,
Hence,
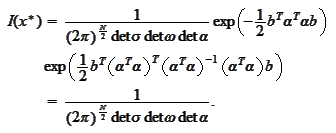 Therefore
Therefore
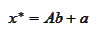 is the mean of the resulting normal distribution. Consequently, we introduce
is the mean of the resulting normal distribution. Consequently, we introduce
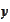 such that
such that
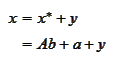 and
calculate
and
calculate
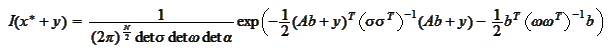
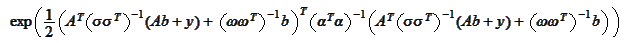
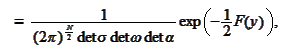
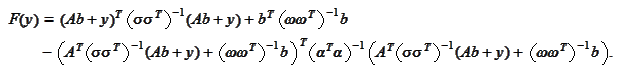 The
The
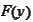 is a quadratic function and we already know that
is a quadratic function and we already know that
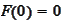 ,
hence
,
hence
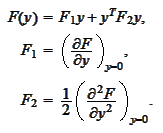 We
have
We
have
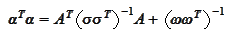
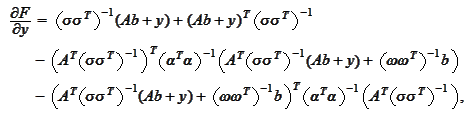
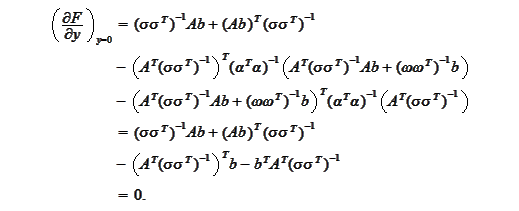
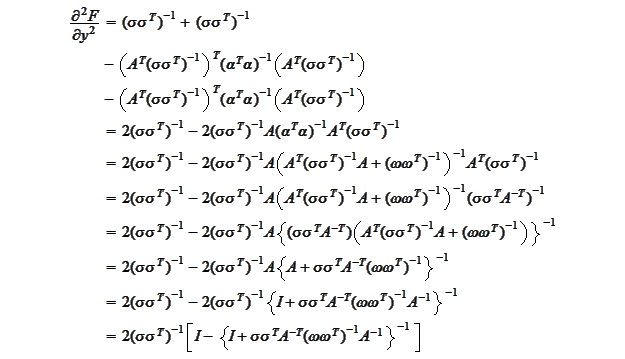
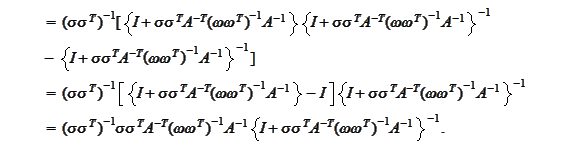 Hence, the covariance of the result is the inverse of the above
expression:
Hence, the covariance of the result is the inverse of the above
expression:
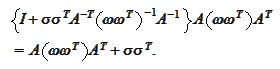 Therefore, we may state the result
Therefore, we may state the result
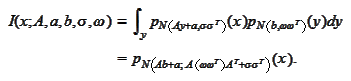
|