e are considering a problem of
forecasting of a random variable
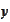 based on information contained by some vector
based on information contained by some vector
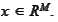 The
The
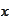 is treated as a sample of some random variable that we also denote as
is treated as a sample of some random variable that we also denote as
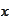 .
.
If the information
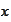 is sufficiently large then it makes sense to look for
is sufficiently large then it makes sense to look for
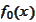 among linear functions:
among linear functions:
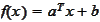 .
Repeating the above argument, we
have
.
Repeating the above argument, we
have
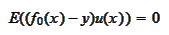 with linear
with linear
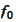 and
and
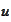 .
.
We extend the above requirement to the case of a vector valued variable
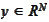 .
We require that the function
.
We require that the function
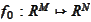 ,
,
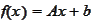 ,
for some matrix
,
for some matrix
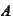 ,
would be such that for any linear
,
would be such that for any linear
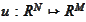 ,
the random quantities
,
the random quantities
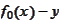 and
and
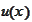 are not
correlated:
are not
correlated:
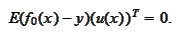 We see that the forecasting operation
We see that the forecasting operation
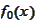 is similar to a linear projection of
is similar to a linear projection of
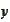 on
on
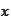 .
This motivates introduction of the
operation
.
This motivates introduction of the
operation
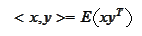 that takes two vector valued random variables and produces a deterministic
matrix. We would like to treat this operation as a scalar product even though
it does not have a full set of properties. We will construct a projection
operation
that takes two vector valued random variables and produces a deterministic
matrix. We would like to treat this operation as a scalar product even though
it does not have a full set of properties. We will construct a projection
operation
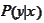 with the defining
properties
with the defining
properties
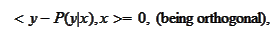
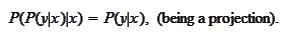 We proceed to verify that the projection
We proceed to verify that the projection
 may be defined by the straightforward adaptation of the formula from the
elementary
geometry
may be defined by the straightforward adaptation of the formula from the
elementary
geometry
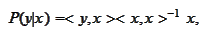 on a subclass of random variables with zero mean:
on a subclass of random variables with zero mean:
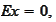
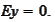 Indeed,
Indeed,
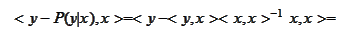
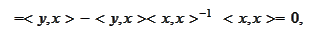 and
and
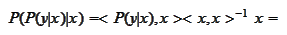
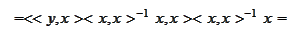
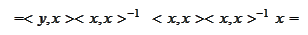
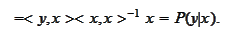
From the
two properties, verified here, all the other well known properties of
orthogonal projection follow. This allows using of geometric intuition in the
computation that follows.
The operation
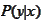 is well defined if the matrix
is well defined if the matrix
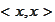 is not degenerate. This is certainly so if the random variable
is not degenerate. This is certainly so if the random variable
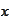 has zero mean because then
has zero mean because then
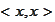 is the covariance matrix of
is the covariance matrix of
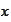 .
However, if
.
However, if
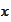 is deterministic then
is deterministic then
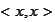 is degenerate. Therefore, we represent a random variable
is degenerate. Therefore, we represent a random variable
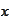 as a sum
as a sum
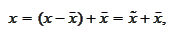 where
where
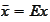 and
and
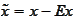 .
Observe that for two vector valued random variables
.
Observe that for two vector valued random variables
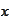 and
and
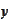
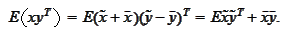 Therefore,
Therefore,
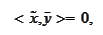 for any
for any
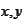 .
Hence, we extend the definition of
.
Hence, we extend the definition of
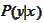 to random variables with non-zero mean by
orthogonality:
to random variables with non-zero mean by
orthogonality:
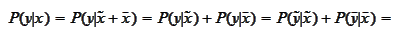
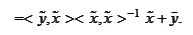 Here we used the fact that the
Here we used the fact that the
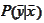 must satisfy
must satisfy
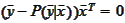 with
with
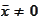 .
The only way this can happen is if
.
The only way this can happen is if
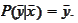
One can verify that this is a maximal likelihood forecast if
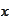 and
and
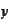 are jointly normal. To see this it is enough to use a jointly normal
distribution function to compute a conditional distribution of
are jointly normal. To see this it is enough to use a jointly normal
distribution function to compute a conditional distribution of
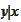 .
In the section (
Kalman filter II
) we
will take such approach.
.
In the section (
Kalman filter II
) we
will take such approach.
|