his section follows
[Hamilton]
. The time
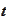is discrete:
.
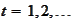Suppose the random variables
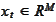and
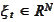are given by the recursive
relations
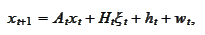
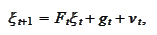where the
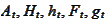are
some deterministic functions of time
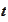of appropriate dimensionality. As usual the
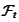denotes the algebra of events representing the amount of information,
available at time
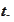The Gaussian random variables
,
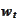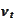are
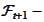measurable
and independent from all
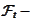measurable
variables of this setup. We understand such situation as variables
,
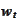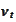being in the future of the time moment
.
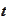We will use this property heavily without further reference. The variables
,
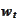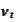have zero mean and known covariance matrixes
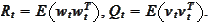The variable
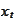is observable. As time progresses we accumulate values
.
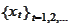The variable
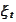is not observable.
We introduce notation
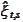for estimation of value
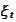based on information
.
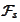Denote
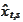forecast of
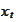based on
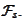Also,
.
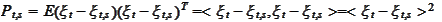Initially, at time
,
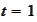we are given values
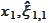and
.
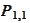Our goal is to determine recursively the quantities
,
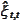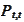as the information
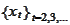flows in.
|
