Note that if an estimate of the
form
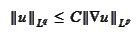 holds with a constant
holds with a constant
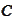 independent of
independent of
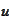 then
then
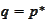 .
Such conclusion follows from the substitution of
.
Such conclusion follows from the substitution of
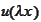 in place of the
in place of the
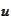 .
.
Proof
Since
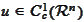 has compact support we
state
has compact support we
state
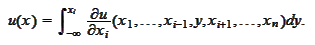 Hence,
Hence,
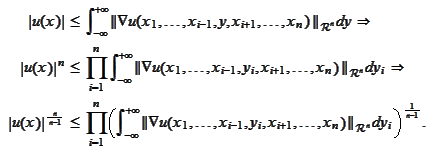 Consequently,
Consequently,
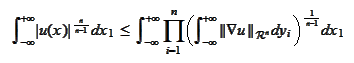 The
The
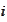 -th
term of the product is independent of
-th
term of the product is independent of
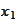 ,
hence, we
continue
,
hence, we
continue
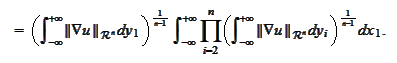 Note that according to the formula (
Holder
inequality
2
),
Note that according to the formula (
Holder
inequality
2
),
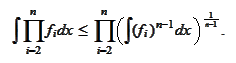
|
|
(HI1)
|
We apply the last relationship with
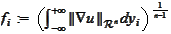 and
obtain
and
obtain
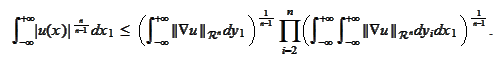
Next, we integrate the above relationship with respect to the
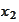 :
:
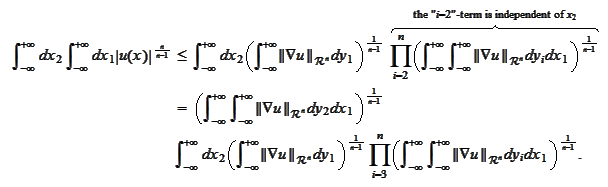
We apply the formula (
HI1
) to the
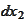 -integral
with
-integral
with
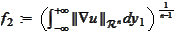 and
and
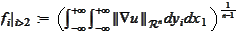 and
obtain
and
obtain
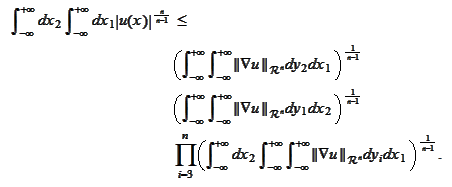
Next, we integrate with respect to the
 :
:
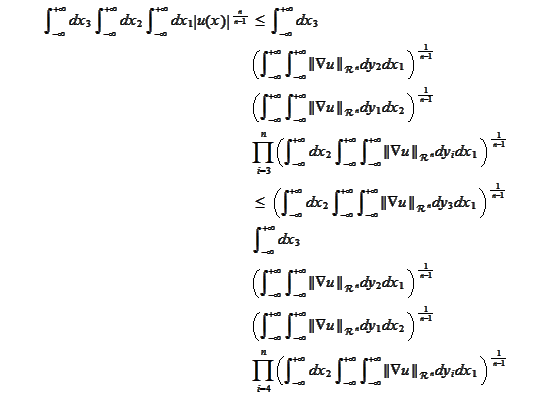 and apply the formula (
HI1
) to the
and apply the formula (
HI1
) to the
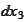 -integral
with
-integral
with
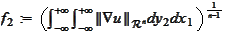 ,
,
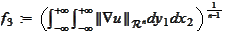 and
and
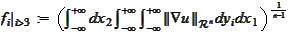 :
:
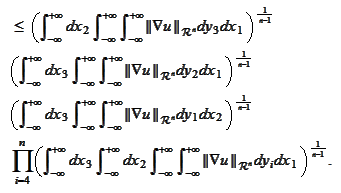 We continue the integration with respect to the variables
We continue the integration with respect to the variables
 ,...,
,...,
 and arrive to the
estimate
and arrive to the
estimate
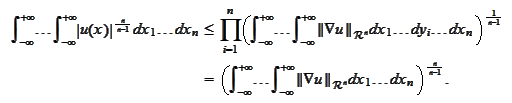 The above is the desired estimate for
The above is the desired estimate for
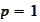 .
.
To obtain the estimate for
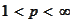 it is enough to apply the last result to the function
it is enough to apply the last result to the function
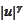 with
with
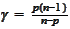 .
.
|