n this section we present a procedure for construction of dual wavelets with
orthogonality across scales. The disadvantage of this construction is
non-compactness of support for one of the wavelets
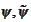 .
In the section
(
Compactly
supported smooth biorthogonal wavelets section
) we present a pair
.
In the section
(
Compactly
supported smooth biorthogonal wavelets section
) we present a pair
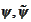 with compact support but without orthogonality across scales (property (d)
below).
with compact support but without orthogonality across scales (property (d)
below).
Proof
of (b),(c),(d). We define
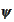 and
and
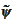 the same way we did in the definition (
Dual
wavelets
). We get biorthogonality of
the same way we did in the definition (
Dual
wavelets
). We get biorthogonality of
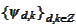 and
and
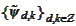 by the proposition (
Dual wavelets
properties
)-f. We also have (
Dual
wavelets
properties
)-a,d,e:
by the proposition (
Dual wavelets
properties
)-f. We also have (
Dual
wavelets
properties
)-a,d,e:
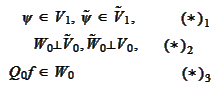 and (a) of the present
proposition:
and (a) of the present
proposition:
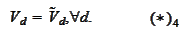 From
From
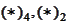 and
and
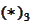 we get
we get
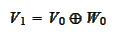 and
and
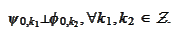 Then, by the formula (
Property
of scale and transport
2
),
Then, by the formula (
Property
of scale and transport
2
),
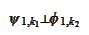 and by
and by
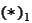
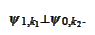 Then, by the formula (
Property
of scale and transport
2
),
Then, by the formula (
Property
of scale and transport
2
),
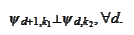 Thus (b) and (c). The (d) follows because, by proposition
(
Dual wavelets properties
)-f,
Thus (b) and (c). The (d) follows because, by proposition
(
Dual wavelets properties
)-f,
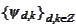 and
and
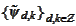 are bases in
are bases in
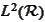 .
.
|